Faculteit van Letteren en Wijsbegeerte
Akademiejaar 1992-1993
Een Onzichtbaar Muziekinstrument
Boekdeel 2
Hoofdstuk 2
-
Proefschrift ingediend tot het behalen van de graad van
Doktor in de Kunstgeschiedenis en Oudheidkunde, richting Muzikologie,
door Godfried-Willem RAES
Promotor: Prof.Dr.Ferdinand DE HEN
Boekdeel 2
HOOFDSTUK 2:
Ultrasoontechnologie
(klik op paginanummers)
| 2.0. | Doel | p.3 |
| 2.1. | 'Holosound 1': historiek en verslag van 16 jaar technisch & artistiek onderzoek | p.4 |
| 2.1.1. | Voorgeschiedenis | p.4 |
| 2.1.2. | Konceptie van een eerste prototype | p.6 |
| 2.2. | Analyze en bespreking van de werking | p.7 |
| 2.3. | Technische realizatie gedetailleerde beschrijving van de schakelingen met metingen en optimalizatieprocedures | p.17 |
| 2.3.1 | De zenders | |
| 2.3.1.0 | Technische eisen | p.17 |
| 2.3.1.1 | Piezo-transducers Zenderschakelingen | p.18 |
| 2.3.1.2 | Capacitieve transducers | p.27 |
| 2.3.1.3 | Ionen en plasma stralers Ionen schakeling | p.29 |
| 2.3.1.4 | Induktieve transducers | p.32 |
| 2.3.2 | De ontvangers | |
| 2.3.2.0 | Technische eisen | p.33 |
| 2.3.2.1 | Piezo-transducers | p.33 |
| 2.3.2.2 | Electret-transducers | p.34 |
| 2.3.2.3 | Condensatormikrofoons | p.34 |
| 2.3.2.4 | Meetmikrofoons en niet geteste types | p.35 |
| 2.3.2.5 | Induktieve mikrofoons | p.35 |
| 2.3.2.6 | De ontvangerschakelingen | p.36 |
| 2.3.2.6.1 | Amplitude-demodulatie | p.36 |
| 2.3.2.6.2 | Phase Locked Loop | p.37 |
| 2.3.2.6.3 | Frekwentie-demodulatie | p.39 |
| 2.3.2.6.4 | Hoogfrekwente voorversterker | p.42 |
| 2.3.3 | De analoge komputer | |
| 2.3.3.1 | Multipliers | p.45 |
| 2.3.3.2 | 'Real-time' analoge rekeneenheid | p.47 |
| 2.3.3.3 | De analoge komputer | p.49 |
| 2.3.3.3.1 | Ingangstrap | p.52 |
| 2.3.3.3.2 | Analoge vermenigvuldiging | p.54 |
| 2.3.3.3.3 | Analoog verschil van kwadraten | p.55 |
| 2.3.3.3.4 | Analoog kwadraat | p.56 |
| 2.3.3.3.5 | Afsluitblok | p.57 |
| 2.3.3.3.5.1. | limiter-kompressor | p.57 |
| 2.3.3.3.5.2. | laagdoorlaatfilter | p.58 |
| 2.3.3.3.5.3. | lijnversterker | p.58 |
| 2.3.3.3.6 | Voeding | p.59 |
| 2.3.3.3.7 | Patching | p.61 |
| 2.3.4 | Evaluatie | |
| 2.3.4.1. | Simulatie | p.63 |
| 2.3.4.1.1 | Legende Muzikale reprezentatie der simulaties | p.67 p.69 |
| 2.3.4.1.2 | Grafische simulaties van bewegingsmodellen | p.70 |
| 2.3.4.1.2.1 | Type 1: Vlottende beweging kurves muzikale reprezentatie kurves |
p.71 p.73 p.74 p.77 |
| 2.3.4.1.2.2 | Type 2: Expanderende beweging | p.85 |
| 2.3.4.1.2.2.1. | Sub-type 1: Teatrale botsing Projektie β-kurve amplitude & β-kurve snelheid ARII-kurve Notentranskriptie ARII0-kurve & ARIIf-kurve |
p.86 p.86 p.87 p.88 p.89 p.92 |
| 2.3.4.1.2.2.2. | Sub-type 2: Explosie of botsing ARCF0-kurve AFCFf-kurve HRCF-kurve Notentranskriptie |
p.94 p.96 p.97 p.98 p.99 |
| 2.3.4.1.2.3 | Type 3: Kontraherende beweging | |
| 2.3.4.1.2.3.1. | Sub-type 1: Imploderende beweging Projektie ARGG-kurve HRGGf-kurve |
p.102 p.102 p.103 p.104 |
| 2.3.4.1.2.3.2 | Sub-type 2: Evaderend Projektie ARFGf-kurve ARFG0-kurve |
p.105 p.105 p.106 p.107 |
| 2.3.4.1.2.4 | Type 4: Gesloten beweging | p.108 |
| 2.3.4.1.2.4.1. | Sub-type 1: Metrische impuls Projektie, β-kurve ARIA-kurve ARIAf-kurve | p.108 p.109 p.110 |
| 2.3.4.1.2.4.2. | Sub-type 2: Perkussieve impuls Projektie, β-kurve ARII-kurve ARIIf-kurve Notentranskriptie |
p.111 p.111 p.112 p.113 p.114 |
| 2.3.4.2: | Metingen dynamiek en signaal/ruisverhouding rezolutie |
p.117 |
| 2.4. | Artistieke prezentatie als muziekteater | p.119 |
| 2.5. | Midi-implementatie: bespreking en kritiek van een brok hardware | p.121 |
| 2.6. | Besluit | p.125 |
HOOFDSTUK 2:
Ultrasoontechnologie
2.0: Doel
In dit hoofdstuk zullen we volgende doelstellingen trachten te bereiken:
1. De technische werking van Doppler-ultrasoontechnologie voor lezers die niet of niet meer zo goed vertrouwd zijn met de elementen uit de fyzika zo precies mogelijk te verklaren of in herinnering te brengen.
2. Een verslag uitbrengen van eigen onderzoek naar de mogelijkheid om gebruik makend van ultrasoontechnologie een non-impakt instrument op te bouwen. Daarbij zullen we, met een detaillering die enerzijds de kontrole door derden (wetenschappelijkheidsvereiste) en anderzijds het nabouwen (toepasbaarheidsvereiste), moet mogelijk maken, de diverse komponenten die daarbij noodzakelijk zijn beschrijven. Ook experimenten die een negatief rezultaat opleverden, worden daarbij behandeld.
3. Aanduiden welke rezultaten werden geboekt en waar onze technische ontwerpen in dit stadium verschillen van gelijkaardige ontwerpen uit de literatuur.
4. Een eerste en zeer beperkte artistieke toepassing van een eerste door ons gerealizeerd non-impakt instrument beschrijven: 'Holosound'.
5. Aantonen, op grond van een elementaire signaalanalyze, dat het beschreven instrument in dit stadium van technische realizatie reeds geluiden produceert die in een aantal van hun parameters -meer bepaald vektoriele frekwentiebandbreedte en amplitude- een korrelatie vertonen met de motorische handelingen waardoor ze worden veroorzaakt.
6. Op grond hiervan en gesteund door de rezultaten van een komputersimulatie-model aantonen dat het instrument als meet-instrument in het kader van onderzoek naar motorische expressie relevant is en bruikbaar kan zijn.
2.1.: Holosound 1
2.1.1.- Voorgeschiedenis
Omstreeks 1975, en nadat we reeds een ruime ervaring en een berg frustraties hadden opgedaan inzake bouw en ontwerp van allerhande alternatieve impakt- en non-impakt elektronische muziek-instrumenten, verscheen een materiaal op de konsumentenmarkt dat o.a. het zelf experimenteren met ultrasonen mogelijk kon maken: keramisch piezoelektrisch materiaal (PXE in het technisch afkortingenjargon).
| Het verschijnsel van de piezo-elektriciteit was op zich reeds sedert het begin van de eeuw bekend. Onder ander het Seignette-zout vertoonde deze eigenschap. Kristallen ervan werden onder meer sedert lang gebruikt in goedkope platenspelers, oortelefoontjes en de zogenaamde kristalmikrofoons. Deze kristallen waren echter heel moeilijk zelf in een elektrische schakeling te gebruiken vanwege de problemen verbonden met de hechting van de aansluitdraden op de kristallen. Bovendien zijn deze kristallen in zeer hoge mate hygroskopisch (vochtgevoelig) en temperatuurafhankelijk. Verder is hun frekwentieweergave niet alleen allesbehalve lineair, maar bovendien ook bijzonder onvoorspelbaar. Het nieuwe keramische materiaal betekende op dit punt een enorme sprong voorwaarts. |
Het betreft een gepolarizeerd ferroelektrisch keramisch halfgeleidermateriaal dat op een erop uitgeoefende druk reageert met het genereren van een elektrische spanning. Het materiaal is wat dit betreft volstrekt omkeerbaar, wat betekent dat een erop aangelegde elektrische spanning een vormverandering (kontraktie of uitzetting, al naar gelang de polariteit van de aangelegde spanning tegenover de polarizatie van het PXE-materiaal zelf) met zich brengt. Gezien de vrij brede frekwentiekarakteristiek van het materiaal (mede afhankelijk van de vorm waarin het wordt gemaakt of versneden) bleek het ideaal voor de bouw van allerhande kontaktmikrofoons. De massa van de mikrofoon kon immers heel klein gehouden worden (van groot belang wanneer men de akoestische klank van het via kontaktmikrofoons te versterken instrument wil behouden) en de signaalafgifte evenals de dynamiek bleek relatief groot te zijn.
| Voor technische specifikaties is het nuttig het Philips Data Handboek, boekdeel 16, 'omponents and Materials: Piezoelectric ceramics & Permanent magnet materials' of een recentere update daarvan te raadplegen. (Onze uitgave: Philips, Eindhoven, januari 1982). In de industrie wordt PXE onder andere gebruikt als aansteker-element in gasverbranders, waar het via een mechanische impuls een vonk van zo' 2000 Volt opwekt. Omgekeerd, als mechanisch trillerelement, wordt PXE gebruikt in ultrasone reinigingsmachines, emulsifieerders, ultrasone lastoestellen voor kunststoffen en metalen... |
Een van de vele materiaaleigenschappen van dit PXE is, dat het kan worden gestemd, en dit zowel gebruikmakend van de fyzisch-mechanische eigenschappen van het materiaal zelf (net zoals men een stuk hout tot een gestemde xylofoon-staaf kan verwerken) als gebruikmakend van de elektrisch-dynamische eigenschappen. Elektrisch gezien gedraagt het PXE gebruikt als transducer zich immers zoals een netwerk samengesteld alsvolgt:
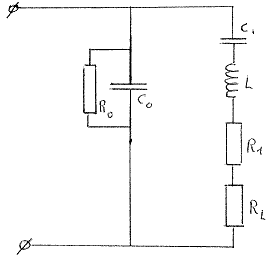 |
Co= kapaciteit van het ingeklemde stuk PXE-materiaal R0= dielektrisch verlies van het PXE R1= mechanisch verlies in het PXE RL= de akoestische of mechanische belastingsweerstand van het PXE-materiaal gebruikt als transducer. C1, L worden gevormd door de massa en de stijfheid van het materiaal. (ref.: Philips Data Handbook, Op.cit, p.A9 - oktober 1980 evenals J.W. Waanders, 'Piezoelectric Ceramics', 1991, p.9) |
Op grond hiervan is het mogelijk PXE materiaal ook te stemmen op ultrasone frekwenties. De impedantiekarakteristiek in funktie van de frekwentie ziet eruit alsvolgt:
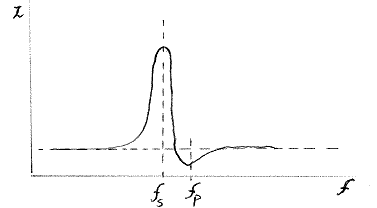
Het punt fs geeft in deze grafiek de serie-resonantie van de kring weer, terwijl fp de parallel-resonantiefrekwentie toont. Beide punten liggen, volgens onze eigen metingen aan piezoschijfjes gekleefd op een messing plaatje, ongeveer een terts uiteen. De mate van resonantie kan zowel worden geaksentueerd door de transducer aan een externe resonantiekring te koppelen, als gedempt door hem 'kortgesloten' te gebruiken.
De grootte van deze resonantiepieken hangt ook af van het type PXE materiaal dat gebruikt wordt.
De eerste praktische experimenten die we opzetten, in 1976, maakten gebruik van het door Philips geproduceerde PXE materiaal PXE5. We gingen daarbij uit van enkele eenvoudige schakelingen voor ultrasone alarmsystemen gepubliceerd in een 'application note' van hetzelfde bedrijf.
| Cfr.: Van Randeraat J. & Setterington, R.E. "Piezoelectric Ceramics", Eindhoven 1974, p. 78-103. Het recentere werk van J.W. Waanders (1991) -een geaktualizeerde uitgave van dat van Van Randeraat- bekwamen we pas nadat het grootste deel van deze studie reeds was gesachreven. |
De schakelingen werkten weliswaar, maar de muzikale mogelijkheden vanzodra we probeerden er veel meer mee te doen dan simpelweg van op afstand en via beweging schakelaars te openen en te sluiten zoals dat bij alarmsystemen gebruikelijk is, lieten sterk te wensen over. We kregen te maken met enorme problemen met de opgewekte ruis en de kleine gevoeligheid. Gegeven de transducers waarover we beschikten (PXE-disks) bleek het systeem slechts relevante bewegingsinformatie op te leveren wanneer de bewegingen plaatsgrepen binnen een hemisfeer met een straal van 50cm van de ultrasone zender.
Pas enkele jaren later verschenen de eerste ultrasone transducers voor gebruik in lucht op de komponentenmarkt. Een relatief ruim gamma aan ultrasone mikrofoons en transducers waarbij het Japanse Murata een van de belangrijkste producenten was. Later kwam daar Toko Inc. bij.
Toepassingen lagen in eerste plaats op de gebieden industriele automatisering en alarmsystemen. Aan de studie van de diverse alarmsystemen en afstandsbedieningen waarin gebruik wordt gemaakt van ultrageluid als medium, hebben we sedertdien vrij diepgaand onderzoek gewijd, omdat we in deze toepassingen aanknopingspunten zagen voor wat we wilden kunnen bouwen.
| Ons artistiek en filozofisch werk rond bellen, sirenes en andere akoestische signaalbronnen waarop we ook in hoofdstuk 1 reeds alludeerden, werd ook in grote mate beinvloed door deze studie. Het leidde tot de reeks muziekautomaten 'Bellenorgel', 'Beltotem' , 'Beltelefoon' en 'Sirene'. |
2.1.2.: Koncept
Het koncept zoals ons dat -bij de aanvang van onze eerste experimenten met ultrasoontechnologie voor ogen stond-, dus vooraleer er sprake was van deze studie en zeker de gegevens die we prezenteerden in ons eerste hoofdstuk, stelden we op schrift als dokumentatie, omdat het de verklaring (motivatie en justifikatie) vormt van heel wat in dit stadium door ons uitgevoerde experimenten. We voegden het -geladen als het is met artistieke opties en persoonlijke vizies die geen onmisbaar verband houden met de wetenschappelijkheid van ons onderzoek- niet toe aan deze studie, maar verwijzen ervoor naar het artikel 'Holosound' dat we in 1990 publiceerden in het tijdschrift 'elesta' evenals naar ' personal story of music and technology' , in het tijdschrift 'Leonardo' , uit 1992.
2.2.: Teoretische analyze van de werking van 'HOLOSOUND'
Holosound was als 'work in progress' en in zijn eerste ontwikkelingsfaze, een experimenteel instrument dat iedere beweging van zijn bespeler onmiddellijk vertaalt in een analoog klank-verschijnsel. Omdat dit klankverschijnsel heel erg specifiek is, het betreft immers gekleurde ruisbanden, kan het geen aanspraak maken op universele muzikale bruikbaarheid, wel integendeel, beschouwden we het als dermate specifiek dat we de naam die we het gaven eveneens gebruikten voor de muziekteatrale kompositie waarbij we het oorspronkelijk inzetten evenals voor de 'audio-art-installaties' die we ermee bouwden. Het principe ervan berust op wat wel eens ultrasone bewegingshologrammen wordt genoemd genoemd.
| De term werd voor het eerst door Wolf Dieter Trüstedt gebruikt: zie appendix sub 5.2.4 |
Een zender opgesteld op een bepaald punt in de ruimte stuurt ultrasone, dus voor de mens onhoorbare geluidsgolven uit. Zolang binnen de door het geluid bestreken ruimte niets beweegt, gebeurt er niets en is er helemaal niets te horen. Vanzodra echter iets beweegt binnen de ruimte, dan wordt de ultrasone akoestische golf -afhankelijk van de richting van de beweging en haar snelheid- in frekwentie omhoog of omlaag gemoduleerd. De bespeler bevindt zich binnen deze ruimte en het is de oppervlakte van zijn lichaam in beweging die door het feit dat het, zoals elk oppervlak trouwens, klank reflekteert, oorzaak is van deze frekwentieverschuivingen. Dit principe berust geheel op wat men in de fyzika het Doppler effekt heeft gedoopt.
Beschouwen we even de hand van de speler en laten we veronderstellen dat deze die hand op een bepaald ogenblik aan een snelheid van 5 meter per sekonde rechtlijnig beweegt. Onderstel voorts dat de ultrasone zender geplaatst binnen dezelfde ruimte, een geluidsfrekwentie heeft van 100kHz. Onderstel verder dat we naast de zender een mikrofoon, gevoelig voor het beschouwde frekwentiegebied opstellen als waarnemer (als mensen kunnen wij immers niet rechtsreeks ultrasonen waarnemen). De frekwentieverschuiving gemeten in de richting van de beweging kunnen we dan berekenen als volgt:
| Opmerking: in al onze formules gebruiken we, daar waar de 'klassieke' notatie typografische problemen zou opleveren, een op komputers meer gebruikelijke notatie, o.m. zoals gebruikt in alle versies van Basic programmeertalen. Dus * voor vermenigvuldiging, / voor deling, \ voor restloze deling, ^ voor machtverheffing. |
-
- stel de geluidssnelheid v = 343m/s
- relatieve geluidssnelheid in de richting van de beweging : 343m/s + 5m/s = 348m/s
- procentuele verschuiving : 101,457% ( + 1,457%)
- 'waargenomen' frekwentie:
100kHz * 101,457% = 101.457Hz - Verschiltoon :
101.457Hz - 100.000Hz = 1.457 Hz
Merk op dat deze verschiltoon, 1457kHz, binnen het gewone audio-bereik valt! Rechtstreeks waarneembaar is hij desondanks echter niet voor een menselijke waarnemer.
| Dit is -terloops gezegd- overigens een mooi experimenteel bewijs voor de stelling waarvolgens som en verschiltonen bij de audioperceptie ontstaan en dus niet in de 'objektieve' werkelijkheid als luchtdrukfrekwentie aanwezig zijn. De signaalsterkte van deze berekende verschiltoon is immers beslist voldoende groot om door het menselijk oor waargenomen te worden. |
Maar, ook gezien vanuit de tegenovergestelde richting wekt de beweging een evengrote verschiltoon op, nml :
-
- 2. relatieve geluidssnelheid tegen de richting van de beweging in :
343m/s - 5m/s = 338m/s - 3. procentuele verschuiving : 98,54% (-1,46%)
- 4. waargenomen frekwentie:
100kHz * 98.54% = 98.542Hz
Verschiltoon :
100.000 - 98.542 = 1.458Hz
- 2. relatieve geluidssnelheid tegen de richting van de beweging in :
Dit kan uiteraard ook in één stap berekend worden met volgende rekenkundige formule:
(1) fdiff = |(fz*((vg +vb)/vg))-fz|
= fz * (vb/vg)
waarin dan:
-
fdiff = de opgewekte verschiltoon
fz = de ultrasone zenderfrekwentie
vg = de geluidssnelheid
vb = de bewegingssnelheid
| Hierbij moet wel de konditie vb << vg worden gesteld. In woorden uitgedrukt, de bewegingssnelheid dient veel kleiner te zijn dan de snelheid van het geluid. |
Hieruit blijkt dat de verschiltonen dezelfde frekwentie hebben wanneer de waarnemingspunten in het verlengde liggen van de richting van de beweging en dus onderling een hoek vormen van 180 graden. Wanneer de ultrasone zender en de ontvanger als het ware in eenzelfde punt opgesteld worden, en de beweging ervoor plaatsvindt geldt:
fdiff = 2 * fz * ( vb / vg )
| Om dit goed in te zien volstaat het de Doppler redenering alsvolgt in twee stappen te beschouwen: Het bewegend objekt ontvangt op zijn oppervlak een geluidssignaal waarvan de frekwentie ten opzichte van die van het vaste zendersignaal verschoven is met fz(vg/vb). Het reflekterend oppervlak wordt vervolgens opnieuw als een geluidsbron gezien, in beweging tegenover de ontvanger, en dus geldt opnieuw een Dopplerverschuiving van fz(vg/vb). De uiteindelijk frekwentie-verschuiving is dus tweemaal de Dopplerverschuiving. |
Om nu de richting van de beweging in klank om te zetten, volstaat het de waarnemingspunten onder een andere hoek op te stellen. Na wat rekenwerk blijkt dat een opstelling van waarnemingspunten onderling en ten opzichte van de zender onder een onderlinge hoek van 60 graden, een optimale ruimtelijke differentiatie mogelijk maakt.
De (tot bewegingen binnen een vlak vereenvoudigde) wiskundige vergelijkingen voor de som en verschiltonen worden dan afgeleid alsvolgt :
de virtuele snelheid van de beweging gezien vanuit het punt O (de ontvanger of waarnemer) wordt dan gegeven door:
Vvirt=Vabs * ¦cos(α)¦
en aangezien fo1, de frekwentie van de verschiltoon, evenredig is met V, de snelheid, geldt ook:
fo1=fmax * ¦cos(α)¦
Beschouwen we nu onze experimenteel als optimaal bevonden opstelling van de waarnemingspunten binnen een gelijkzijdige driehoek waardoorheen de beweging plaatsgrijpt en noemen we de bewegingshoeken vanuit elke ontvanger o1, o2, o3, dan α1, α2, α3 dan volgen de diverse frekwenties en hun samenhang uit :
f1=fmax * |cos α1|
f2=fmax * |cos α2|
f3=fmax * |cos α3|
en, wanneer we voor α1, α2 , α3 telkens alleen de scherpe hoeken beschouwen:
α1 + α3 = π/3 ( rad.)
α1 + α2 = 2 * π/3
en dus geldt ook :
f1 ¦cos α1û¦ f2 ¦cos α2û¦ f1 ¦cos α1¦
--=-------- --=-------- --=--------
f2 ¦cos α2û¦ f3 ¦cos α3û¦ f3 ¦cos α3¦
fmax is hierin dan de frekwentie van de verschiltoon zoals we die zouden kunnen opvangen indien de beweging loodrecht zou staan op de as van de betreffende ontvanger. Zij valt eenvoudig te berekenen uit de 'absolute' bewegingssnelheid en de vaste zenderfrekwentie.
Wiskundig kunnen hieruit dan volgende relaties (2) , (3) en (4) tussen de frekwenties onderling worden afgeleid:
Uit α1+α3 = π/3 volgt dat cos(α1+α3) = cos(π/3) = 1/2
en:
(cos(α1)*cos(α3))-(sin(α1)*sin(α3))=1/2
(cos(α1)*cos(α3))-(1/2)=sin(α1)*sin(α3)
(cos(α1)*cos(α3))-(1/2) =((1-cos2(α1))^(1/2))*((1-cos2(α3))^(1/2)
(cos2(α1)*cos2(α3))+(1/4)-cos(α1)*cos(α3) = 1-cos2(α1)-cos2(α3)+(cos2(α1)*cos2(α3))
cos2(α1)+cos2(α3)-(cos(α1)*cos(α3)) = 3/4
Waaruit we afleiden:
(2) f12+f32- f1*f3=(3/4)*fmax2
Voorts volgt uit α1 + α2 = (2/3)*π dat :
cos(α1+α2)=cos((2/3)*Pi) = -(1/2)
waaruit volgt:
(3) f12+f22+(f1*f2)=(3/4)*fmax2
Door nu (2) en (3) gelijk te stellen komen we tot een bijzonder en welhaast estetisch eenvoudig verband tussen de onderlinge toonhoogtes:
f12+f32-(f1*f3) = f12+f22+(f1*f2)
of:
f32-f22 = (f1*f2)+(f1*f3)
of nog:
(f3-f2)*(f3+f2) = f1*(f2+f3
waaruit tenslotte volgt:
f3-f2 = f1
(4) f3 = f1+f2
| Merk op dat deze betrekking alleen geldt voor gevallen waarbij de beschouwde bewegingsvektor in het vlak gevormd door de drie waarnemingspunten valt. Anders gezegd, wanneer de beweging tweedimensioneel is tegenover de waarnemingspunten, verkrijgen we ook slechts 2 van elkaar onafhankelijke parameters. We zullen verder in dit hoofdstuk een driedimensionele benadering verder uitwerken. Ook alle later aan de orde komende wiskundige analyzes, steunen op ons komputersimulatieprogramma 'Holosimi' dat wel degelijk 3-dimensioneel werkt. (cfr. appendix, 5.2.2). Dat we ons hier beperken tot een 2-dimensioneel model spruit alleen voort uit onze bekommernis zo duidelijk mogelijk te zijn wat betreft de principiele werking en de wiskundige achtergrond. |
Meetkundige tekening ter illustratie:
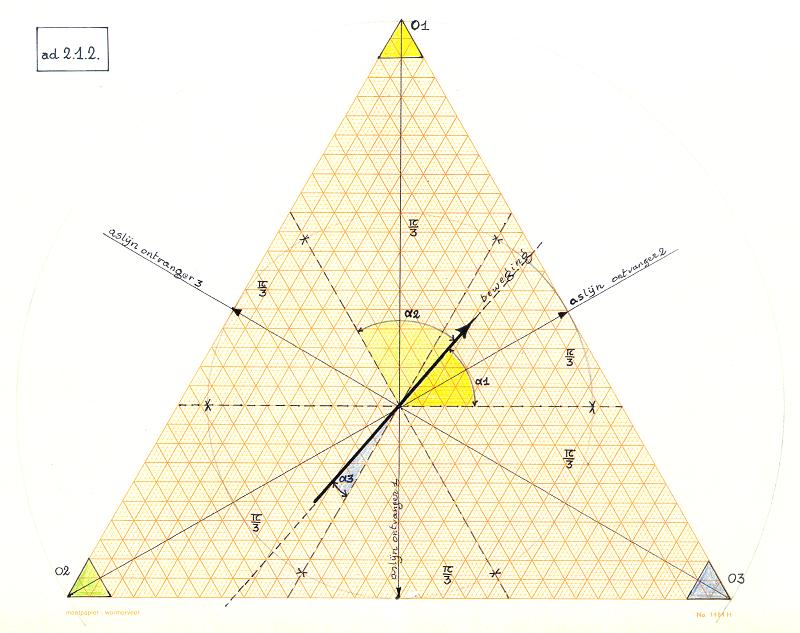
Technisch probleem dat zich onmiddellijk stelt wanneer we op grond van bovenstaande wiskundige overwegingen een uitsluitend door lichaamsbeweging te bespelen instrument wilden bouwen, is dat de berekende verschiltonen niet akoestisch bestaan noch als dusdanig waargenomen worden door menselijke waarnemers. Hier diende dus de analoge elektronische rekentechniek ingeschakeld te worden. In eerste instantie poogden we gebruik te maken van allerhande schakelingen zoals die werden ontwikkeld voor -overigens erg onbetrouwbare- alarmsystemen en dieptemeters uit de scheepvaarttechniek. Bijna al deze schakelingen berusten echter op een of andere vorm van amplitude-demodulatie (alarmen) of pulsvertragingstijdmeting (dieptemeters en echografen). De signalen worden in deze technische toepassingen immers alleen gebruikt om logische nivoos te genereren. Bovendien bleek de haalbare signaal/ruisverhouding voor muzikale doelen volkomen onaanvaardbaar. Na toch wel enkele jaren van nogal intensief laboratoriumwerk (zie verder voor een samenvattend verslag), hebben we uiteindelijk volgend schakelprincipe als optimaal weerhouden. De 'clou' van de schakeling bestaat enerzijds in het oneigenlijk gebruik van gebalanceerde modulatoren als frekwentie-demodulatie-schakelingen, voor een signaal dat eigenlijk geen echt frekwentiemodulatiesignaal is, en anderzijds in de manier waarop de demodulatoren onderling gekoppeld werden. Voor de niet-technische lezer kunnen we voorlopig wellicht volstaan door de werking van de gebalanceerde modulator te definieren als een elektronische schakeling die van twee op de ingangen aangeboden elektrische spanningen met een bepaalde frekwentie steeds alle som en verschiltonen tussen die frekwenties opwekt en op de uitgang aanbiedt. Ook de uit de vroegere elektronische muziek welbekende ringmodulator berust op deze schakeling.
De overdrachtfunktie van zo'n modulator ziet eruit alsvolgt:
Uout=(Ux1-Ux2)*(Uy1-Uy2)/10V
voor twee sinusvormige ingangssignalen en Ux2=-Ux1 , Uy2=-Uy1 (dit is immers het geval wanneer de schakeling gebalanceerd wordt uitgestuurd ) wordt dit dan :
(5) Uout=(2*Ux1)*(2*Uy1)/10V
of nog:
(6) Uout=(2*(Uxmax*sin(2*π*fx*t))*(2*Uymax*sin(2*π*fy*t)))/10V
In werkelijkheid krijgen we in deze toepassing echter niet twee signalen op de ingangen te zien, maar wel op elke ingang de som van twee signalen: de zenderfrekwentie plus het daaraan toegevoegd Doppler-verschoven signaal. De overdrachtfunktie wordt dan ook verkregen door in formule (5) de termen Ux en Uy te substitueren door:
(7) Ux1= Uzmax*sin(2*π*fz*t)+Uxmax*sin(2*π*fx*t)
Uy1= Uzmax*sin(2*π*fz*t)+Uymax*sin(2*π*fy*t)
waarin dan Uz en fz resp. de ontvangen maximumspanning en de frekwentie van de draaggolf zijn, en Ux, fx en Uy, fy respektievelijk spanning en frekwentie van de Doppler-verschoven komponent in het signaal.
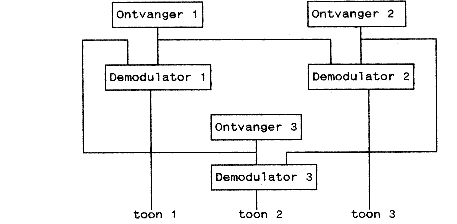
De teoretische en sterk vereenvoudigde overdrachtfunkties voor deze schakeling zijn dan:
- Uitgangssignalen van de ontvangers :
- Uoa=Uzmax*sin(2*π*fz*t)+Uamax*sin(2*π*fa*t)
- Uob=Uzmax*sin(2*π*fz*t)+Ubmax*sin(2*π*fb*t)
- Uoc=Uzmax*sin(2*π*fz*t)+Ucmax*sin(2*π*fc*t)
- Ingangssignalen van de demodulators:
- Demodulator 1 : Uoa en Uob
- Demodulator 2 : Uob en Uoc
- Demodulator 3 : Uoc en Uoa
Uout2=(2*Uob)*(2*Uoc)/10V
Uout3=(2*Uoc)*(2*Uoa)/10V
Waarin: Uz , fz :resp. spanning en frekwentie van de zender
Uoa , fa :resp. spanning en frekwentie van het verschoven signaal op de eerste ontvanger
Uob , fb :id. voor de tweede ontvanger
Uoc , fc :id. voor de derde ontvanger
In het uitgangssignaal blijft bij praktische schakelingen een betrekkelijk sterke zendersignaalkomponent aanwezig, evenals heel wat nevenfrekwenties op veelvouden daarvan. Deze konden echter op eenvoudige wijze met een lagere orde filterschakeling weggefilterd worden, gezien de grote afstand - in frekwentie - tussen het gewenste uitgangssignaal en deze bijprodukten.
De praktische opbouw van de schakeling wanneer men een muzikaal aanvaardbare signaal ruisverhouding wil halen in de orde van de 60dB stelt de uiterste eisen inzake precizie aan de gebruikte onderdelen en aan de afregeling. Voor de opbouw werd in de recentste versies dan ook gebruik gemaakt van precizie instrumentatieversterkers en 'laser-trimmed analog multipliers' van de firma Analog Devices (type AD632). Ook de bouw en ontwikkeling van de ontvangers was niet direkt een triviale aangelegenheid. Er bestaan weliswaar piezolelektrische ultrasoon ontvangers in de handel (o.m. van Murata, Japan) , maar die zijn elektrisch zowel als mechanisch gestemd op een welbepaalde werkfrekwentie (meestal 40kHz) en hebben een betrekkelijk kleine bandbreedte en een soms enorme non-lineariteit (zie verder). Twee bruikbare types kwamen na lang zoeken uit de bus: enerzijds mechanisch gedempte en elektronisch gelinearizeerde piezoelelektrische ontvangers, anderzijds zelfgebouwde kondensatormikrofoons, waarvoor echter een nogal grote externe voedingsspanning nodig is waardoor ze moeilijk te miniaturizeren vallen. Op dit vlak kan verdergaand onderzoek wellicht nog veel aan de goede werking verbeteren.
Het instrument werkt in principe met eender welke ultrasone toonhoogte, waarbij het duidelijk zal zijn dat naarmate men deze toonhoogte hoger kiest, het frekwentiebereik van de ontstane verschiltonen ook groter zal zijn. Hier zijn echter zeer grote praktische beperkingen aan verbonden: immers naarmate men de toonhoogte laat stijgen is er, voor het bestrijken van een evengrote ruimte, een akoestisch afgestraald vermogen nodig dat niet evenredig stijgt met de toonhoogte, maar wel met minstens de derde macht daarvan!
Bij de laagste in dit instrument bruikbare ultrasone frekwentie van circa 34kHz volstaat een elektrisch zendervermogen van 2 Watt ruimschoots.
Bij 200kHz is algauw zowat 35Watt nodig, en in de praktijk nog heel wat meer , wat dan te wijten is aan de geringe efficientie van ultrasone stralers in lucht bij deze frekwentie. Een bijkomend probleem is dat geluid naarmate de frekwentie toeneemt, direktioneler wordt afgestraald, wat nogmaals bijdraagt tot een noodzakelijke vermogensverhoging. Middels toepassing van een kaskade van ultrasone zenders zó dat een voldoende sferische straler bereikt wordt, is dit wel te verhelpen. Op een bepaald punt echter worden hierbij grenzen kwa ultrasone geluidsdruk overschreden waarbij helemaal niet meer voor zeker kan worden aangenomen dat ze voor de mens ongevaarlijk zijn.
Bovenstaande akoestisch-wiskundige en technische overwegingen zijn uiteraard sterk simplifierend en inleidend. Zo dienen we er bvb. toch op te wijzen, dat het in werkelijkheid onmogelijk is om een 'zuivere' toon te produceren, maar dat steeds 'kleurruis' met min of meer duidelijke toonhoogte ontstaat. Dit laat zich makkelijk verklaren uit het feit dat waar we in onze aanvankelijke analyze uitgingen van een bepaalde bewegingssnelheid, dit in de praktijk niet kan bestaan. Immers, wanneer een mens een lichaamsdeel beweegt, dan beweegt elk punt ervan aan een verschillende snelheid: wanneer je met de armen zwaait blijven de schouders min of meer op hetzelfde punt. Derhalve zijn de voortgebrachte verschiltonen ook de som van alle gereflekteerde frekwenties, m.a.w. klusters of ruisbanden.
Een tweede opmerking geldt het feit dat de sterkte van de opgewekte geluiden recht evenredig is met de grootte van het bewogen oppervlak. Dit effekt is echter muzikaal uitstekend te gebruiken omdat het perfekt aansluit bij de relatie expressie-beweging van de mens. Het instrument zet de snelheid van de beweging om in de toonhoogte van een kluster of ruisband. Een lineaire beweging geeft aanleiding tot een min of meer konstante toon, terwijl een versnelling een stijgende glissando wordt, een vetraging een dalende. De intensiteit van de beweging (de hoeveelheid lichaam die beweegt), wordt omgezet als de geluidssterkte van die kluster. Bovendien geschiedt alles vektorieel , d.w.z in funktie van de richting van de beweging.
Wanneer nu de luidsprekers waarop de rezulterende klanken ten gehore worden gebracht in een driehoekige opstelling waarbinnen de luisteraar zich moet bevinden worden geplaatst, dan hoort deze laatste als het ware akoestische bewegingshologrammen: de klanken -in funktie van de bewegingen die hen veroorzaken- bewegen zich overeenkomstig door de akoestische ruimte.
Projektie van de speelruimte van 'Holosound' in de luisterruimte waarbinnen de toehoorders zich bevinden:
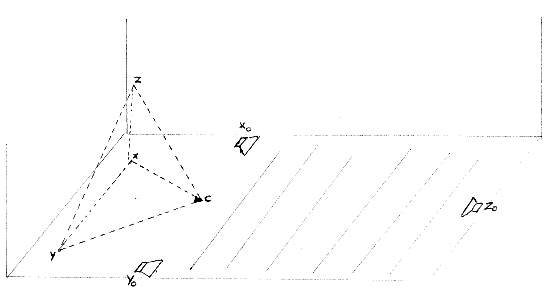
Een eerdere mogelijkheid waatoe het instrument zich in deze vorm gemakkelijk leent, ontstaat wanneer we de zender uitvoeren als een ultrasone FM-zender, waaraan we een extern signaal als modulatiesignaal toevoeren. Gezien de aard van het instrument is als modulatiesignaal daarvoor de stem van de speler-beweger het meest voor de hand liggend. De toonhoogtes van dit modulatiesignaal zullen dan in frekwentie veranderen in funktie van de beweging van de spreker/zanger.
| Met een dergelijke konfiguratie experimenteerden we naar aanleiding van een muziekteaterproduktie onder de titel 'Piramisch' in samenwerking met plastisch kunstenaar Herman Schepens in 1986. |
Ook konfiguraties waarbij het uitgangssignaal wordt teruggekoppeld naar de modulatieingang van de zender, leveren verrassende muzikale rezultaten op, die dan echter nagenoeg volledig afhankelijk zijn van de akoestische ruimte waarin het instrument wordt opgesteld. Op een dergelijk dynamisch systeem kunnen de klassieke lineaire wiskundige beschrijvingstechnieken niet langer worden toegepast, maar dienen we ons wiskundig apparaat in de richting van niet lineaire vergelijkingen te gaan zoeken. De Lorenz-vergelijkingen zijn daarvan naast de Mandelbrot fraktals uit de zgn. Chaos-teorie, wellicht de best gekende voorbeelden. 'Standing Waves', een live-elektronische kompositie uit 1984 kwam op deze wijze tot stand.
Die ruimte bepaalt overigens ook bij normale rechttoe-rechtaan werking in hoge mate het klankrezultaat. De bedoelde en in het instrument geimplementeerde funkties komen teoretisch slechts korrekt uit de bus, wanneer we het instrument gebruiken in het akoestisch vrije veld (in een vlakke onbebouwde ruimte), of in een anechoïsche ruimte. In de praktijk echter valt ook in normale niet te kleine koncertzalen, een en ander nogal goed mee. Hoe kleiner en meer reflekterend de ruimte, hoe geringer het ruimtelijk effekt van het Holosound instrument is, en ook hoe kleiner de precizie waarmee de klanken vanuit de bewegingen kunnen worden gestuurd.
2.3.: Gedetailleerde beschrijving van de ontwikkelde en geteste schakelingen
Een samenvattend laboratoriumverslag
2.3.1: Ultrasoon-zender ontwerpen
2.3.1.0: Technische eisen
Ons eerste probleem bij het opzetten van experimenten met bovenbeschreven opstelling was het bouwen van een deugdelijke geluidsbron voor ultrasonen.
Schakelingen voor dergelijke toestelletjes worden industrieel toegepast in alarmsystemen evenals o.m. in autofocus fototoestellen waarin ze gebruikt worden voor de automatische scherpstelling (afstandsmeter). De in deze toepassingen gebruikte moderne schakelingen bleken echter niet zomaar bruikbaar voor ons doel en dit omwille van het niet voldoen aan een aantal van de hiernavolgende eisen:
- - zuiver symmetrisch en liefst sinus-vormig signaal
(vervorming <= 0.1%)
- Assymmetrieën in het afgestraalde signaal leidden bij de ontvangst en na demodulatie tot een grotere ruiskomponent.
- - temperatuuronafhankelijkheid van de frekwentie
- Aangezien de gebruikte ontvangerschakelingen bij voorkeur rond de gebruikte centrale ultrasoonfrekwentie afgestemde versterkers bevatten, uiten fluktuaties in de zendfrekwentie door temperatuurdrift zich onvermijdelijk als amplitudemodulaties in het uitgangssignaal, die niet drager zijn van enige relevante informatie. Technisch gesproken dus, laag-frekwente ruis.
- - lage ruis (<= -90dB)
- Bedoeld is hier de eigen ruis aanwezig in het uitgestuurde zendersignaal.
- - hoge signaalsterkte
- Hoe hoger het opgewekte en uitgestuurde signaal, hoe groter ook het signaal bij de ontvangers en hoe beter ook de signaal/ruisverhouding in het eindrezultaat.
- - geschiktheid voor kontinu gebruik (geen pulsen, zoals in gebruikelijke industriele 'sonar-ranging' systemen).
- Het vermogen dat een transducer kan verwerken is niet alleen een funktie van het maximaal eraan toe te voeren signaal, maar ook van de toelaatbare tijdsduur waarin de transducer aan dat signaal mag worden blootgesteld. (De dissipatie-faktor). In sonar-systemen zoals die worden gebruikt in de toestellen voor ultrasone afstandsmetingen en in die voor dieptepeilingen in het water, worden de zenders op een fundamenteel andere manier gebruikt dat wat wij hier beogen. Immers in sonar systemen wordt een heel sterke maar korte ultrasonore puls uitgestuurd, en vervolgens wordt de tijd gemeten tussen het uitsturen van de puls en de ontvangst van de echo (de door een hindernis weerkaatste golf). De informatie over de positie van de hindernis, volgt uit deze tijdsinformatie en de voortplantingssnelheid van de geluidsgolf door het betreffende medium. Bij gepulseerd gebruik mag de aan de transducer toegevoerde energie tot een faktor 100 hoger liggen dan bij kontinu gebruik als zender.
- - afstembaarheid van de toonhoogte
- De afstembaarheid van de toonhoogte is geen kriterium of vereiste in verband met de kwaliteit, wel met de mogelijke optimalizatie in funktie van de penetratiegraad, de direktionaliteit en de gevoeligheid van het uiteindelijke systeem. Wanneer de zenderfrekwentie wordt gewijzigd, dient dat overigens ook in de ontvangers te gebeuren.
- - temperatuuronafhankelijkheid en algemene stabiliteit van de amplitude van het uitgezonden signaal
- Ook hiervoor geldt dat elke amplitude onstabiliteit in het zendersignaal, als ruis op de uitgang zal verschijnen. De gevoeligheid hiervoor is echter aanzienlijk verbeterd sedert we FM-demodulatietechnieken zijn gaan toepassen in de demodulatiefaze.
- - omnidirectionele afstraalkarakteristiek
- Hier krijgen we te maken met de akoestische wetten als beperkende faktor. Immers het is een fysisch feit dat een geluid naarmate de frekwentie hoger is, ook gerichter wordt afgestraald. Wanneer het ultrasoon geluid afkomstig is van een resonerend fysisch voorwerp (zoals bvb. piëzoelektrisch kristal of een membraan) dan kan de zender alleen omnidirectioneler worden gemaakt, door de zender uit meerdere 'punt'-vormige stralers samen te stellen. Uiteraard wordt hij dan groter. Ook is dit niet echt een bevredigende oplossing omdat bovendien rekening moet gehouden worden met een onderlinge fazegelijkheid van de afgestraalde geluidsgolven. In de praktijk is zoiets bijzonder moeilijk te verwezenlijken. We menen dit probleem ten dele te hebben opgelost door gebruik te maken van ionenstralers als bron van ultrasoon geluid. (zie verder).
We zullen hier in funktie van de geformuleerde eisen en bemerkingen, de praktische mogelijkheden verder analyzeren en de rezultaten meedelen van onze experimentele bevindingen terzake.
2.3.1.1: Piezoelektrische ultrasoontransducerschakelingen
Hiermee worden dan de schakelingen bedoeld waarin gebruik wordt gemaakt van de ons sedert 1976 praktisch bekende piëzoelektrische komponenten.
Hoewel het op zich genomen perfekt mogelijk is piezoelektrische transducers zelf te vervaardigen uitgaand van het ruwe materiaal, en hoewel we dat aanvankelijk ook zelfs hebben gedaan, is en blijft het een bijzonder tijdrovend en precies werkje, wanneer men tenminste een rezultaat wenst te bekomen dat op voorhand binnen nauwe grenzen was bepaald. Voor wie het toch wil proberen, wijzen we erop dat de techniek van het manueel stemmen van piezomateriaal veel gelijkenissen vertoont met het stemmen van kristallen zoals die gebruikt worden in de hoogfrekwenttechniek: beetje bij beetje afslijpen met polijstpasta om de frekwentie te verlagen, stukjes afbreken of lateraal slijpen om de frekwentie te verhogen. Wanneer de juiste en gewenste frekwentie bereikt is, dient het elektrisch geleidend laagje aangebracht te worden (elektrisch geleidende zilverlijm is goed bruikbaar) evenals de aansluitdraadjes. Het piezomateriaal is veel zachter en ook brozer dan het kwarts in de kristallen, wat het werk eigenlijk alleen maar nog moeilijker maakt.
Gezien de beschikbaarheid tegenwoordig van afgewerkte produkten op dit vlak, piezoelektrische transducers voor gebruik in lucht of andere gassen, is het vandaag beter en makkelijker daarvan uit te gaan. Indien nodig, kan nog altijd een bestaand produkt getrimd worden in de richting van een gewenste waarde. De transducers die door het Japanse bedrijf Murata worden aangeboden bestaan uit een vierkantig blokje (5mm x 5mm, dikte ca. 0.8mm)) PXE materiaal waarop in het centrum een kleine metalen konus, gestemd op de nominale frekwentie, is gekleefd. Deze konus beinvloedt vooral het afstraalgedrag van de tranducer omdat hij de faze-opheffing van de signalen vanuit verschillende hoeken van het stukje PXE uitsluit.
- eenvoud en kommerciële verkrijgbaarheid
- hoge efficiëntie
- miniaturizeerbaarheid
- matige frekwentiestabiliteit
- de frekwentie hangt af van de temperatuur (omgevingstemperatuur zowel als de temperatuursverhoging als gevolg van de eigen dissipatie in de transducer)
- geringe afstembaarheid
- Deze moet indien gewenst mechanisch gebeuren zoals hoger geschetst.
- relatief grote vervorming van het signaal
- geringe lineariteit
- De signaalafgifte, bij konstante frekwentie van het toegevoerde signaal verloopt niet lineair met de toegevoerde amplitude. De signaalafgifte bij konstante amplitude maar veranderlijke frekwentie is vanwege de primaire en sekondaire resonanties die in het PXE optreden, alles behalve lineair te noemen.
- temperatuurgevoelig
- geringe belastbaarheid
- geringe keuze in frekwenties
- Deze transducers zijn op de onderdelenmarkt niet of nauwelijks verkrijgbaar voor de hogere frekwentiegebieden ( > 80kHz). De meest koerante waarde is 40kHz. Ook verkrijgbaar zijn 28kHz, 34kHz, 36kHz, 45kHz, 50kHz, 66kHz. De transducers voor hogere frekwenties worden uitsluitend aangeboden voor gebruik in vloeistoffen of vaste stoffen. Frekwenties gaande van 100kHz tot 4MHz zijn dan verkrijgbaar. Deze transducers worden gebouwd voor gebruik in schepen (sonar-dieptepeilingen) en medische instrumentatie (echografie). Voor de laagste ultrasone geluiden kunnen eventueel ook piezo-hoorntweeters gebruikt worden. Deze zijn bruikbaar tot ca. 35kHz, hoewel hun frekwentieweergavekurve er in dit gebied uitziet als een kam.
Praktische door ons gebouwde en geteste piezo-schakelinhen voor gebruik als ultrasoonzender:
1.Opbouwschemas voor ultrasoonzenders gebruikmakend van een oscillator-chip (555) als frekwentiebepalende komponent:De berekening van alle schakelingen waarin gebruik gemaakt wordt van de 555 chip - een der meest koerante en populaire chips in laagfrekwente oscillatortoepassingen- is uitermate eenvoudig.
Het output-signaal is een blokgolf waarbij de HOOG-tijd en de LAAG-tijd berekend wordt alsvolgt:
Thoog = 0.693 * (R11 + R2) * C1
Tlaag = 0.693 * R2 * C1
De periode-tijd is dan ook Tp = Thoog + Tlaag of,
Tp = 0.693 * (R1 + (2 * R2)) * C1
en dus de frekwentie: fo = 1 / Tp.
| De gedetailleerde specifikaties voor de diverse chips van de 555 familie, kunnen weergevonden worden in de data-books van fabrikanten zoals National Semiconductor, Exar, Texas Instruments e.a. Een goede bron voor diverse toepassingen van deze chip vormt ook CARR, Joseph, "C Timer Handbook", 1981. Cfr. verder, Horowitz & Hill,"The Art of Electronics", 1980/81, p.164-165). |
Het enige ontwerptechnische probleem met deze chip wordt gesteld door het feit dat hij een enkelvoudige voeding dient te krijgen (maximaal +18V) en zijn toepassing wanneer rond 0V gesymmetreerde uitgangsspanningen gewenst worden, wat extra onderdelen kost.
Een algemene opmerking aangaande deze chip die dient gemaakt te worden, heeft betrekking op de extra ontkoppeling die nodig is in de voeding, wat veroorzaakt wordt door de sterke 'spikes' die de oscillator op de voedingslijnen zet. Dit was er bij vele van onze eerste proeven oorzaak van dat heel wat van het zendersignaal in onze analoge komputerschakeling via de voeding binnensloop en daar aanleiding gaf tot heel wat lek-problemen. De modernste versies van de 555-klassieker maken echter intern gebruik van CMOS-transistoren en kennen dit probleem omzeggens niet meer.
Ultrasoon-zender schakeling, met twee alternatieve mogelijkheden voor de uitvoering van de eindtrap.
Het tweede alternatief levert een meer sinusvormig, maar kleiner, uitgangssignaal:
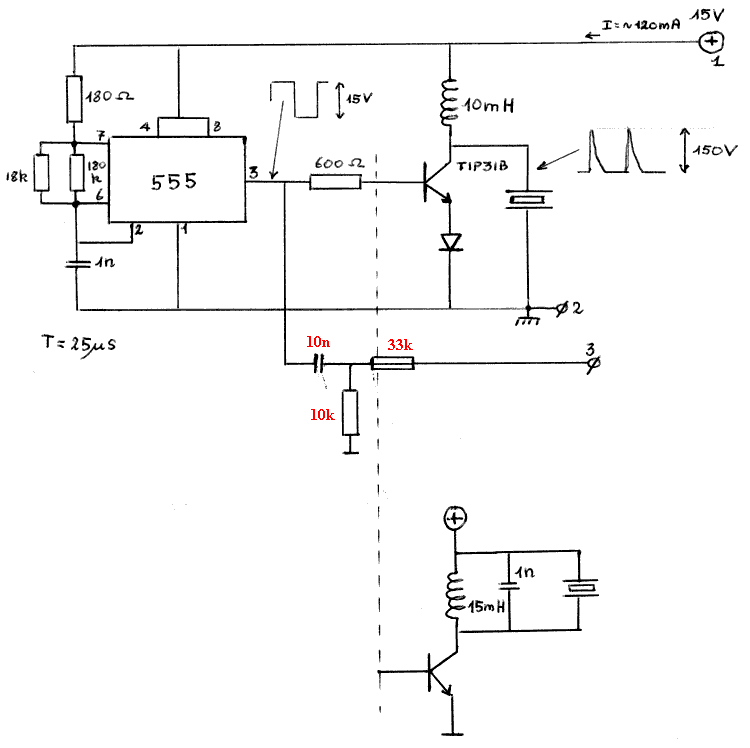
Volgend schema geeft uitstekende rezultaten, maar maakt gebruik van een transformator (gevormd door een standaard Toko-spoeltje te voorzien van een extra primaire wikkeling) voor de koppeling van de oscillator aan de transducer. Wanneer standaard 40kHz transducers gebruikt worden, levert deze schakeling het absoluut maximum toelaatbare vermogen aan de zenders. Wanneer de spanning groter wordt dan de hier bereikte 100Vtt, dan geeft de tranducer onherroepelijk de geest.
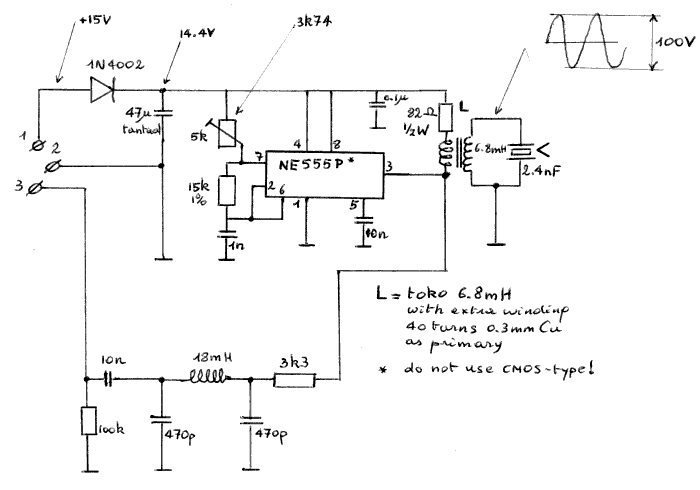
Naar aanleiding van een artistiek-wetenschappelijke manifestatie in het Antwerpse spoorwegstation, werd mij gevraagd om in samenwerking het het Laboratorium voor Fysica van de RUG, de door hen aldaar opgestelde Foucault-slinger (een proef waarmee de aardrotatie wordt aangetoond) te sonorizeren. Het lag voor de hand dat we daarvoor gebruik zouden maken van ons Holosound systeem. Gezien echter de drukke trafiek in een spoorwegstation, was het noodzakelijk de zender in de slinger zelf in te bouwen.
| De muzikale konsekwentie van het plaatsen van de ultrasone geluidsbron op het bewegende lichaam zelf, is dat het Dopplerfrekwentie-verschil nu gegeven wordt door fd= fc * (v / va), dus een oktaaf lager dan wanneer zender en ontvanger vast opgesteld staan terwijl alleen het reflekterend lichaam in beweging is. De ontvangen verschiltoon, gezien het meer puntvormige van de geluidsbron, is veel zuiverder dan in het eerder beschouwde geval. Ook de sub 1.2 geciteerde projekten van Michel Waisvisz gebruiken de ultrasonen op deze wijze. |
De voeding diende dan ook vanuit een zo klein mogelijke batterij te kunnen gebeuren. Uitgaand van de hierdoor gestelde technische vereisten, hebben we toen een variant op bovenstaande schakelingen berekend en ineengezet, werkend op een batterijtje van 9Volt en met een stroomverbruik van slechts 12mA. Als stuurelement wordt hier een vermogens veld-effekt transistor (FET type VN88AF) gebruikt, terwijl voor de '555' een Intersil CMOS-type (7555) werd geselekteerd. De redelijk symmetrische maar niet echt sinusvormige spanning over de transducer heeft een piek-tot-piek waarde van 20Volt. Dit ontwerp is dan ook een optimalizatie voor wat betreft zuinig stroomverbruik en efficientie.
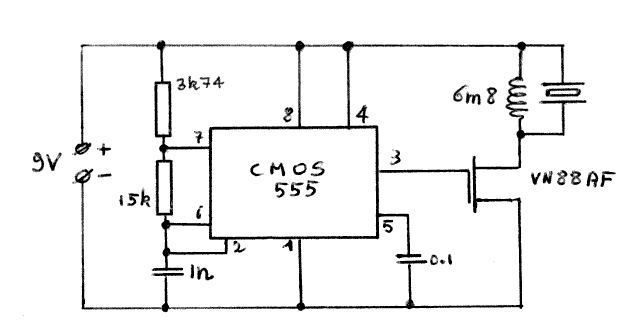
2. Zenders opgebouwd als "Clapp"-oscillator:
Dit type oscillator is zelfoscillerend, d.w.z. de transducer is opgenomen in het frekwentiebepalend netwerk van de oscillator zelf. De schakeling schittert door eenvoud, maar vraagt nogal wat experimenteerwerk na de berekening van de dimensionering alvorens een en ander naar behoren funktioneert. De Clapp-oscillator is eigenlijk een variant op de in de hoogfrekwent-techniek gebruikelijk Pierce-oscillator.
| Cfr. ARRL-Handbook, 1989, p.10-2 voor een ontwerptechische bespreking. |
De sinusvormige wisselspanning over de transducer (dit is een groot voordeel van deze schakeling) kan wanneer spoelen met een hoge Q-faktor worden gebruikt, gemakkelijk tot 70Vtt bereiken. De schakeling kan echter moeilijk in frekwentie regelbaar worden gemaakt.
We geven twee berekende en ook geteste en goed bevonden realizaties, de eerste maakt gebruik van piezotransducers gefabriceerd door Murata (type EFR-OSB 40K241) , de tweede van piezohoorntweeters voor gewone audiotoepassingen geproduceerd door Motorola.
Een praktische moeilijkheid verbonden aan de toepassing van eerste schakeling is dat de transducer elektrisch volledig geisoleerd van de massa en de behuizing dient te worden opgesteld. Dit vergt, bij toepassing van kommercieel verkrijgbare transducer-elementen, een ingreep op hun ontwerp, aangezien hun behuizing bijna steeds een van de twee aansluitingen vormt en er in elk geval elektrisch mee is verbonden.
(Bouwjaar 1981/82)
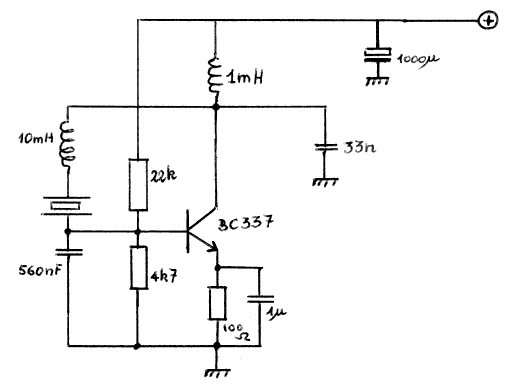
Schakeling gebruik makend van een Motorola hoorntweeter:
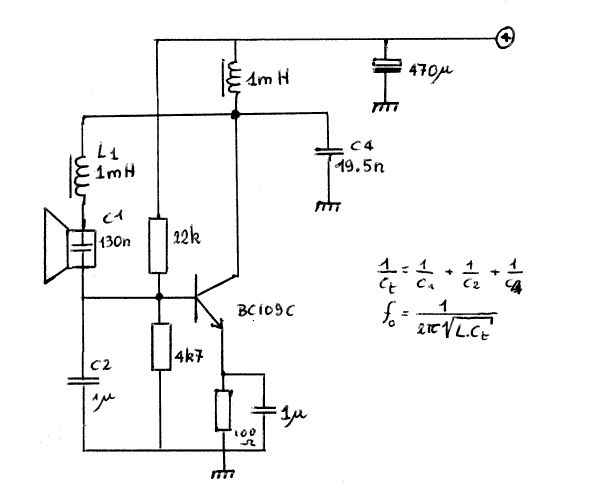
Opmerking: vele van de ontwikkelde zenderschemas geven naast hun ultrasone output ook een elektrisch signaal, synkroon met de akoestische output af. Dit signaal wordt in vele holosound toepassingen gebruikt als referentieinput voor de analoge komputer, wanneer deze wordt ingesteld om voor elke ontvangst- transducer afzonderlijk de verschiltonen fz - fo1,
fz - o2, en fz - fo3 te produceren.
3.-Ultrasone F.M.-zenderTot slot van deze voorstelling van enkele eenvoudige zenders nog een schakeling van een zender die voor ultrasone frekwentiemodulatie-experimenten bijzonder goed werkt. In deze reeds iets komplexere schakeling hebben we gebruik gemaakt van de populaire EXAR funktiegenerator-chip, type XR2206.
De frekwentie van deze zender kan ingesteld worden van 30kHz tot 58kHz. De maximale modulatiediepte is 10kHz (frekwentiezwaai).
Bouwjaar: 1982.
| Voor de formules voor de berekening van de dimensionering van deze schakeling verwijzen we naar de Exar publikatie terzake: Exar Integrated Systems Inc, "Function Generator Data Book", Sunnyvale, California, 1981. |
Schema van de ultrasone F.M.-zender:
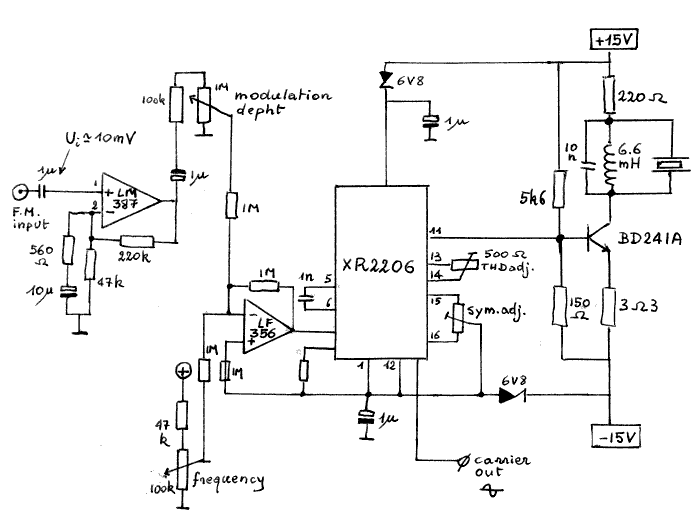
2.3.1.2.: Kapacitieve ultrasoontransducerschakelingen
Voordelen verbonden aan het gebruik van kapacitieve transducers voor ultrasone geluidsbronnen:- redelijk goede lineariteit
- De lineariteit hangt vooral af van de eigenschappen van het membraan en de erop aangebrachte spanning. De eigenfrekwentie van het membraan dient minstens een faktor 100 lager te liggen dan de laagste frekwentie die we willen kunnen afstralen. De spanning op het membraan mag evenwel niet zo klein zijn, dat het niet netjes strak gespannen is. Desondanks treden er echter talloze, in de praktijk onvoorspelbare, komplekse trillingspatronen in het membraan op waardoor de kurve waarbij de frekwentie tegen de afgestraalde geluidsdruk wordt uitgezet, vol pieken en dalen komt te zitten. Ook dient erop gewezen te worden dat de transducer een kondensator is en dus intrinsiek een in funktie van de frekwentie veranderlijke impedantiekurve vertoont.
[ Zc = 1 / (2 * π * f * C) ]
- De lineariteit hangt vooral af van de eigenschappen van het membraan en de erop aangebrachte spanning. De eigenfrekwentie van het membraan dient minstens een faktor 100 lager te liggen dan de laagste frekwentie die we willen kunnen afstralen. De spanning op het membraan mag evenwel niet zo klein zijn, dat het niet netjes strak gespannen is. Desondanks treden er echter talloze, in de praktijk onvoorspelbare, komplekse trillingspatronen in het membraan op waardoor de kurve waarbij de frekwentie tegen de afgestraalde geluidsdruk wordt uitgezet, vol pieken en dalen komt te zitten. Ook dient erop gewezen te worden dat de transducer een kondensator is en dus intrinsiek een in funktie van de frekwentie veranderlijke impedantiekurve vertoont.
- lage vervorming
- Deze is een rechtstreeks gevolg van de geringe massa van het trillende membraan, waardoor de 'ompliance' (volgzaamheid) er groot kan zijn in vergelijking met piezo- of elektromagnetische werkingsprincipes.
- grote frekwentiestabiliteit
- Aangezien het membraan zelf niet gestemd wordt op de voort te brengen frekwentie, is de stabiliteit wat dit betreft uitsluitend een funktie van de gebruikte oscillator-schakeling.
- hoge spanningen nodig voor de uitsturing
- grote gevoeligheid voor vocht en stof
- De diëlektrische eigenschappen van lucht hangen af van de temperatuur en van de vochtigheid.
- temperatuurgevoelig
- laag rendement
Het werkingsprincipe waarop deze tranducers berusten is dat van de elektrostatische luidspreker. Het principe is de eenvoud zelf: een elektrisch geleidend dun en flexibel membraan (gemetalizeerd Mylar o.i.d. bvb.) wordt op een kleine afstand van een geperforeerde stijve plaat gespannen, zo dat tussen beide geen elektrisch kontakt bestaat. Op het gespannen membraan wordt tegenover de bazisplaat een elektrostatische spanning gebracht (1.500 tot zo' 10.000 Volt D.C.), waarop de signaalspanning wordt gesuperponeerd. Deze spanning moet zo hoog mogelijk zijn, maar net niet zo hoog dat vonkoverslag kan optreden. Dit laatste verschijnsel leidt niet alleen tot geknetter en vuurwerk, maar bovendien tot een geperforeerd en onherroepelijk vernietigd membraan.
| Het principe van de elektrostatische luidspreker wordt ook voor gewone luidsprekerinstallaties wel toegepast. Het Engelse 'top-class' merk Quad, levert elektrostatische luidsprekers die tot het allerbeste behoren van wat de markt aan luidsprekers te bieden heeft, waar het om werkelijkheidweergave en niet om brute kracht gaat. Interessante en nuttige aanwijzingen voor het zelf ontwerpen van audio-luidsprekers, overigens door veralgemening van de geboden informatie door ons ook gebruikt als uitgangspunt voor de bouw van ultrasone speakers, staan in een technische monografie over dit onderwerp: WAGNER, Ronald "lectrostatic Loudspeaker, design and construction", Tab Books, Inc., 1987. Deze publikatie die, terloops gezegd een heel goede historische inleiding heeft met betrekking tot het onderwerp geluidsweergevers, leerde ons ook dat de eerste elektrostaten gebouwd werden voor militaire ultrasone toepassingen, reeds in 1912, kort na de ramp met de Titanic, door de Russische fyzikus Chilowski en de Fransman Paul Langevin. Ook in deze toepassing werd het principe echter na korte tijd verlaten ten bate van elektromagnetische en piezo-transducers. Men beschikte in de periode voor de tweede wereldoorlog nog niet over de syntetische materialen die nodig waren voor het maken van een goed membraan. Mylar werd pas in 1949 door DuPont op de markt gebracht. Een materiaal dat in heel wat sektoren van de hedendaagse instrumentbouw later onmisbaar is gebleken.( o.m. trommelvellen!) |
Hoewel we heel wat praktische schakelingen ter evaluatie hebben opgebouwd, bleek geen ervan uiteindelijk een betere prestatie te leveren dan de hiervoor reeds beschreven schakelingen. We gaan op de bouwtechnische details van het schema dan ook niet verder in. Wellicht de belangrijkste reden waarom we ons zoeken in deze richting staakten, heeft te maken met de praktische omstandigheid dat dit type zender relatief groot uitvalt, niet in de eerste plaats vanwege het membraan, maar vooral in verband met de nodige hoge gelijkspanning, wat een grote afstand tussen de komponenten van de voeding noodzakelijk maakt.
2.3.1.3.: Ionen & ultrasoonstralers
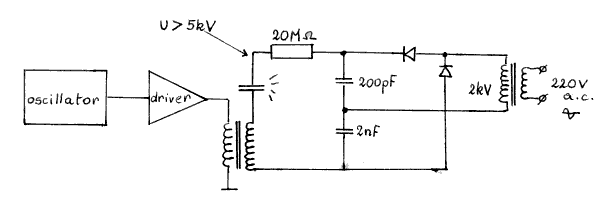
Deze ultrasone stralers zijn wellicht wat 'esoterische' ontwerpen. Eigenlijk gaat het om twee verschillende werkingsprincipes:- Ionen-straler:
-
Deze maken gebruik van het ionen-wind effekt dat kan gemeten worden wanneer een scherpe punt geladen wordt met een heel hoge spanning (25kV en meer!).
Wanneer deze ionen-wind gemoduleerd wordt met een wisselspanning (een audiosignaal bvb.), dan krijgen we een geluidsbron. De gesuperponeerde modulatiespanning dient in elk geval relatief klein te zijn in verhouding tot de ionizerende gelijkspanning.
-
Deze maken gebruik van het ionen-wind effekt dat kan gemeten worden wanneer een scherpe punt geladen wordt met een heel hoge spanning (25kV en meer!).
- Plasma-straler:
- Ook hier wordt gebruik gemaakt van zeer hoge elektrische spanningen. Hier gebruiken we echter twee omgekeerd geladen scherpe punten, waartussen we een vonk trekken. De boog die ontstaat is een elektrisch plasma dat o.m. (via thermische agitatie) een geluidsfront kan veroorzaken wanneer het wordt gemoduleerd met een audio-signaal.
Zelf hebben we dit principe een vijftal jaar geleden gebruikt voor de bouw van een zuiver digitale luidspreker, waarin pulsbreedtemodulatie (PWM) wordt toegepast. (cfr. appendix, 5.2.1 'Talking Flames').
- Ook hier wordt gebruik gemaakt van zeer hoge elektrische spanningen. Hier gebruiken we echter twee omgekeerd geladen scherpe punten, waartussen we een vonk trekken. De boog die ontstaat is een elektrisch plasma dat o.m. (via thermische agitatie) een geluidsfront kan veroorzaken wanneer het wordt gemoduleerd met een audio-signaal.
Beide types stralers hebben we ook als bron van ultrasoon geluid uitgetest. De zuivere ionen-straler hebben we verworpen, omdat hij teveel ruis oplevert. De plasma-straler hebben we slechts enkele keren voor muzikale toepassingen in een holosound kontekst gebruikt. Wel vormde hij de standaard ultrasone straler voor het merendeel van onze metingen aan de ontvangers, en dit omwille van het gemak waarmee hij op verschillende frekwenties kan worden ingesteld enerzijds en omwille van het feit dat het een zuivere rondomstraler is anderzijds. Hierbij dan een overzichtje van de voor en nadelen verbonden aan de plasma-straler:
- Voordelen:
- omnidirektionele puntstraler (plasma)
- lage vervorming
- groot frekwentiebereik
Door de zeer voorspelbare frekwentiekarakteristiek van de plasma-straler, is hij bijzonder geschikt voor frekwentiemodulatie in het ultrasone gebied. - grote frekwentiestabiliteit
De frekwentiestabiliteit is een funktie van externe oscillatorschakelingen, behalve wanneer de plasmaschakeling omwille van de efficientie bvb. zelfoscillerend wordt ontworpen.
- Nadelen:
- gevoeligheid voor luchtbewegingen
Luchtbewegingen in de omgeving veroorzaken onstabiliteit van het plasma, wat zich uit als amplitudemodulatie van het signaal. Na demodulatie klinkt dit als 'popcorn'-ruis en/of gesputter. - gevaarlijk
De gevaren zijn die die in het algemeen onvermijdelijk verbonden zijn aan het gebruik van hoogspanning, ook al is die, althans bij plasma-speakers, betrekkelijk hoogfrekwent en treedt dus het skin-effekt op. Wanneer de boog op het lichaam overspringt, dan leidt dit steeds tot kleine oppervlakkige brandwonden. Deze technologie lijkt daarom geen grote toekomst op het vlak van de konsumentenelektronika weggelegd te zijn. - brandgevaar
Brandbare stofdeeltjes en/of stukjes textiel of papier worden door het plasma aangezogen en ontbranden onmiddellijk. - volumineus
De geluidsbron zelf moge dan al kwazi puntvormig zijn, de schakelingen nodig om haar te doen werken zijn groot omwille van de hoogspanning, de nodige feriettransformator, de koelvinnen voor de schakeltransistoren of MosFets. - inbranding van de elektroden.
Voor onze allereerste experimenten gebruikten we gewone naalden in gehard staal (passerpunten). Deze hadden echter slechts een levensduur van circa 10minuten. Daarna trad er kratervorming op aan de punten die verder geleidelijk afsmolten. Het gebruik van zuivere Worfram-elektroden lostte dit probleem grotendeels op. De levensduur van de elektroden beloopt nu ruimschoots een week bij kontinu gebruik. - inefficiënt
Van de hoeveelheid stroom die in de transducerschakeling gaat wordt meer dan 99.99% omgezet in warmte en slechts een fraktie wordt als geluid afgestraald. Onze prototypes trekken bij een voedingsspanning van 12Volt, een stroom van 12 tot 18 Ampere! - zeer gevoelig voor luchtverontreiniging
Stofdeeltjes in het plasma doen dit laatste knetteren en verstoren de regelmaat van de boog. - etherpolutie
De schakeling is een sterke bron van radiofrekwente storingen. Radio- of TV-ontvangst in de buurt van het toestel is volstrekt onmogelijk. Het gebruik ervan is dus strikt genomen wettelijk verboden. Een kommerciele toepassing zolang hier niets aan wordt verholpen is dan ook uitgesloten. Een oplossing, door ons echter niet getest, zou erin kunnen bestaan het ganse toestel in een fijnmazige kooi van Faraday op te stellen. Het geheel zal er dan evenwel bepaald niet kleiner op worden.
- luchtverontreiniging
De plasma-straler produceert een aanzienlijke hoeveelheid ozon., Het onderzoek naar de mogelijke schadelijke (of heilzame volgens sommige bronnen...) effekten daarvan valt buiten het bestek van dit onderzoek en ook van onze kompetentie. De ozon-produktie kan duidelijk als een geur waargenomen worden.
- gevoeligheid voor luchtbewegingen

2.3.1.4.: Induktieve ultrasone zenders
Wat op het eerste zicht wellicht zowat het meest evidente lijkt, hebben het in deze behandeling voor het laatste overgehouden. Eigenlijk zelfs eerder een beetje 'pro memorie' en alleen omdat ons geen grove nalatigheid zou worden verweten! Maar er zijn goede redenen om dit type transducer hier niet te behandelen:
- het blijkt heel moeilijk ferromagnetische materialen te vinden die ook in het frekwentiegebied tussen 40 en 200kHz nog goed funktioneren als elektromagneet in kombinatie met een membraan. Geen van de elektromagnetische tweeters die we hebben getest, voldeden. Meer nog, alle exemplaren die op onze proefbank terecht zijn gekomen, zijn gesneuveld...
Het probleem lijkt te zijn dat enerzijds om die hoge geluidsfrekwenties te halen een erg klein membraan nodig is, terwijl anderzijds, met het oog op het gewenste vermogen de noodzakelijke spreekspoel toch een zekere massa dient te hebben. Beide eisen samenvoegend komen we tot een teoretische konstruktie waarbij de massa van de spreekspoel een veelvoud is van die van het membraan. Efficient kan een dergelijke konstruktie als ultrasone transducer principieel nooit zijn.
Een tweede probleem is dat de spreekspoel in dit frekwentiegebied een aanzienlijk deel van de toegevoerde energie in de vorm van radiostraling uitzendt, wat voor ons doel uiteraard een pure verliesfaktor betekent.
| Heel onlangs (01/1993) hebben we toch het onderzoek naar induktieve zenders terug geopend, en dit op grond van een idee om in plaats van membraanspeakers, bandtweeters te gaan gebruiken. De experimenten zoals die thans nog lopen gaan daarbij eigenlijk niet uit van luidsprekers, (de band-tweeters die we vroeger poogden te gebruiken gaven allen de geest) maar van omgebouwde en ook omgekeerd gebruikte band-mikrofoons (Beyer), waarin we het bandje pogen af te stemmen -en zelfs extern stembaar te maken- op de gewenste resonantiefrekwentie. |
Besluit: Uit ons onderzoek komen als ultrasone straler de keramische piëzo transducers als meest geschikt naar voor. Merkwaardig genoeg komt voor een keertje de goedkoopste oplossing ook als beste uit de bus.

Foto: realizatie van een elektronische schakeling voor een programmeerbare ultrasoonzender voor 40kHz én 200kHz.
2.3.2: De Ultrasoonontvangers:
2.3.2.0:
De technische eisen te stellen aan de kwaliteit van ontvangers zijn nog vele malen strenger dan diegene die we dienen te stellen aan die van de zender. De ontvangen signalen zijn hier immers bijzonder klein. Vergeten we immers niet dat de ontvangers, wanneer er geen enkele beweging is binnen het bestreken veld, de draaggolf zelf ontvangen. Wanneer een objekt binnen het veld beweegt, dan ontvangt de ontvanger nog steeds deze draaggolf, maar gemengd met een vele malen zwakkere verschiltoon. Zaak is nu, ervoor te zorgen dat deze verschiltoon goed wordt ontvangen en dus niet wordt gemaskeerd door een draaggolf die de ontvanger zou satureren.
De belangrijkste eisen kunnen samengevat worden alsvolgt:
- Signaal/ruisverhouding: >= -66dB
- Gevoeligheid > 50microvolt
- Bandbreedte > fz +/- fdiff
- lineariteit binnen de band
- dynamisch bereik > 120dB
- Richtingskarakteristiek: cardioide
Ook hier hebben we geëxperimenteerd met de meest diverse schakelingen en opnemer-elementen.
Naar eigenschappen van de opnemers, onderzochten we volgende mogelijkheden m.b.t. de gebruikte ontvangst-transducers in praktische schakelingen:
2.3.2.1.: Piëzoelektrische opnemers (Murata)
- Voordelen:
- goedkoop
- grote dynamiek
- goede gevoeligheid
- Nadelen:
- geringe bandbreedte en lineariteit
Het betreft hier in principe identiek dezelfde komponenten als die welke gebruikt worden voor de zender. Alleen zal hier bij de fabrikatie de nadruk niet dienen te worden gelegd op maximale vermogensdissipatie en de temperatuurdrift die daarvan het gevolg is, maar veeleer op de gevoeligheid. De gebruikte stukjes piezokeramiek zullen, gebruikt als ontvanger dus een veel kleinere massa mogen hebben. Overigens worden de zenders en ontvanger door enkele fabrikanten als gekoppelde paren geleverd.
3.2.2.2.: Elektret-ultrasoonmikrofoons
Voordelen:- goedkoop maar moeilijk verkrijgbaar
- Voor onze experimenten maakten we gebruik van een volledige verpakking transducers van dit type die we kochten in een elektronische dump-winkel in de beroemde New Yorkse Canal-street in 1980. (Trans-Am Electronics) De fabrikant van deze komponenten hebben we nooit kunnen achterhalen, en evenmin beschikken we over informatie over gebeurlijke andere leveranciers van gelijksoortige elementen. Wel weten we, op grond van de verpakking, dat de transducers werden gefabriceerd voor gebruik in het Amerikaanse leger. Ook de produktiedatum is ons bekend: 1978. Het frekwentiebereik (-3dB) van onze exemplaren loopt van 25kHz tot 85kHz.
- grote dynamiek
- Onze exemplaren weerstonden een geluidsdruk van 130dbA zonder dat er een merkbare vervorming optrad.
- goede lineariteit en bandbreedte
- cfr. wat daarover hoger werd opgemerkt.
- vochtgevoeligheid
- Dit is een bezwaar dat eigenlijk voor alle kapacitieve opnemers geldig is.
- signaal/ruisverhouding <=-42dB
- Dit cijfer geldt voor normale gebruiksomstandigheden, en dus niet niet bij 130dBA, wat we immers alleen konden bereiken door een zender op enkele millimeters van het mikrofoonkapsel te plaatsen. Dit niet zo geweldige cijfer kan wel verbeterd worden door de impedantietransformatietrap in de kapsule die met een FET is uitgevoerd, te vervangen door een beter en ruisvrijer exemplaar.
2.3.2.3.: Kondensatormikrofoons
De ontdekking dat top-klasse kondensatormikrofoons kunnen worden ingezet voor ultrasone toepassingen deden we eigenlijk helemaal per toeval. We waren op een dag een geluidsopname aan het maken in de opnamestudio, toen daar bij vergetelheid een ultrasone zender was ingeschakeld gebleven na een reeks eerdere experimenten en metingen. Bij het maken van de geluidsbalans bleken alle VU-meters in de studio onwaarschijnlijk hoge geluidssterkten aan te wijzen. Zelfs toen we de musici lieten stoppen, kregen we nog steeds een sterke uitslag van de meters.
Na lang zoeken was de oorzaak in de ingeschakelde ultrasoonzenders gevonden. Het is wellicht belangrijk hierbij te vermelden dat het type kondensatormikrofoon dat wij in de studio gebruiken Schoeps CMC3 en CMC5 is, een mikrofoontype waarin niet van transformatoren voor het sturen van de symmetrische kabels gebruik wordt gemaakt, maar wel van een aktief uitgevoerde drivertrap met diskrete transistoren. Hoewel niet door ons onderzocht, is het niet zeker dat ook kondensatormikrofoons van andere merken (Neumann of AKG bvb.) eenzelfde breed uitgestrekte karakteristiek vertonen. Hoe dan ook is het een eigenschap die in de technische specifikaties van de betreffende mikrofoons niet is terug te vinden.
Vanzelfsprekend hebben we na deze ontdekking onderzoek gedaan naar de mogelijkheden en perspektieven ervan.
- grote dynamiek
- geringe vervorming
- zeer lineair
- De gevoeligheid van de Schoeps mikrofoons neemt wel degelijk af met de frekwentie, maar de kurve verloopt bijzonder geleidelijk, iets wat vrij eenvoudig elektronisch te kompenseren valt.
- goede S/R verhouding
- Hoewel deze beoordeling, gezien de kwaliteit van het type mikrofoon, in de lijn der verwachtingen lag, zijn de S/R waarden in het ultrasone gebied toch niet zo goed als ze zijn voor het hoorbare gebied.
- erg duur
- niet bruikbaar voor frekwenties > 70kHz
- vochtgevoelig
- gevoelig voor normaal audiogeluid.
- Uitgerekend hier zit het grootste probleem verbonden aan het ultrasoon gebruik van deze normale mikrofoons. Weliswaar is het mogelijk alle frekwenties onder 20kHz via een elektronisch filter weg te nemen, maar het ontwerp van een dergelijk filter -rekening houdend met de gewenste lineariteit, lage vervorming en lage signaal ruisverhouding evenals met de wenselijke zeer hoge steilheid van de afsnijkarakteristiek, is bepaald niet van de poes. De komplexiteit ervan weegt zwaar door op het voordeel van de ogenschijnlijke eenvoud verbonden aan het gebruik van 'ormale' mikrofoons. Op zich genomen zou de gevoeligheid voor audio niet zo' groot probleem hoeven te zijn, ware het niet, dat we onze installatie uiteindelijk willen gebruiken voor het implementeren van een muziekinstrument, m.a.w. in een kontekst waarin precies het akoestische eindrezultaat het doel is. Een terugkoppeling van de output naar de input van het systeem is in deze kontekst een verfoeilijke gedachte.
2.3.2.4.: Niet onderzochte transducertypes:
Een aantal fabrikanten van mikrofoons hebben in hun katalogi onder de hoofding meetmikrofoons voor laboratoriumtoepassingen, opnemers vermeld staan die qua specifikaties beslist uitstekend geschikt zouden zijn voor ons doel. (Sennheiser meetmikrofoons bvb.). De kostprijs ervan is evenwel zo hoog dat ze heel beslist niet binnen de financiele mogelijkheden vallen van een individuele onderzoeker met een beperkt budget. Nu hadden we uiteraard dergelijke tuigen op bvb. de Universiteit in bruikleen kunnen vragen, maar een oplossing zou dit niet zijn, aangezien we er minstens 3 stuks nodig hadden en dit bovendien voor een periode van minstens 5 jaar... De vraag ware retorisch geweest.
2.3.2.5.: Induktieve mikrofoons
Volledigheidshalve hebben we ook een heel ruim assortiment aan induktieve mikrofoons (inklusief band-mikrofoons van top-kwaliteit) getest. Geen enkel exemplaar leverde een praktisch en bruikbaar rezultaat op.
2.3.2.6.: De ontvangerschakeling:
2.3.2.6.1: Amplitude-demodulatie
Zoals hoger reeds opgemerkt, zijn we in de zeventiger jaren uitgegaan van de application notes met betrekking tot ultrasone PXE-materialen gepubliceerd door Philips.
Deze application notes behandelen alarmsysteemschakelingen. Uitgaand van deze schakelingen, waarin het gereflekteerde signaal, teneinde de echo te scheiden van de ultrasone draaggolf, een amplitude-demodulatie ondergaat. De schakeling vertoont dan ook een opvallende gelijkenis met die van een klassieke middengolf AM-ontvanger:
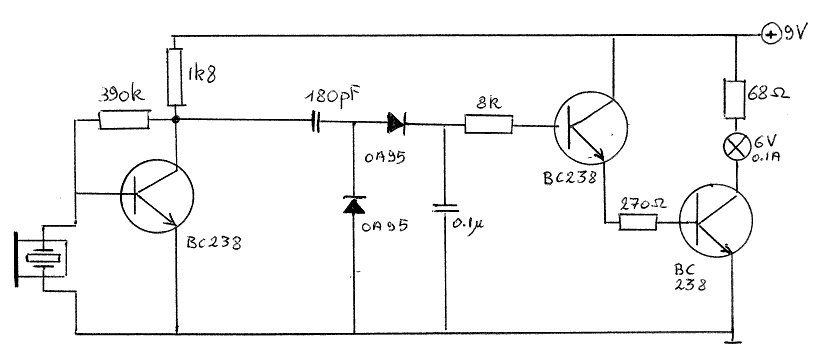
Uit:Van Randeraat, J & Setterington R.E. , "Piezoelectric Ceramics", (1974), p. 96.
In de oorspronkelijke Philips applikatie, stuurt het amplitude gedemoduleerde signaal via een versterkertrapje, een relais dat een alarm in werking stelt. (In het geciteerde schema voorgesteld door een lampje). Anders gesteld, vanuit het echo-signaal wordt uiteindelijk slechts één enkel bit aan informatie overgehouden: was er beweging in een mate groter dan de drempelwaarde of was die er niet. Voor een alarm volstaat dit, zoals voor heel vele industriele sensortoepassingen, uiteraard volkomen. Ons streefdoel bestond er echter in, uit dit signaal precies een maximum aan informatie af te leiden. (cfr. sub 2.2)
Dit heeft dan geleid tot volgende -op de eindtrap na met diskrete komponenten- gebouwde en werkende schakeling, die tevens ook de eerste was die we voor publieke voorstellingen en demonstraties hebben gebruikt (1976-1982).
De ingangstrap is een frekwentie-selektieve voorversterker rond 40kHz en bestaande uit twee transistortrappen. Voor elke verschillende zenderfrekwentie moet de schakeling dus ook anders gedimensioneerd worden. Daarna volgt de amplitudedemodulator, waarvoor gebruik wordt gemaakt van twee gepaarde germanium-diodes in een spanningsverdubbelende schakeling. Na deze demodulatie volgt een met spoelen en kondensatoren opgebouwd π-laagdoorlaatfilter met een afsnijfrekwentie lager dan 10kHz. Het audiosignaal wordt tenslotte in de laatste met een ruisarme op-amp uitgevoerde versterkertrap, tot een gezond 0dBV lijnnivoo opgekrikt.
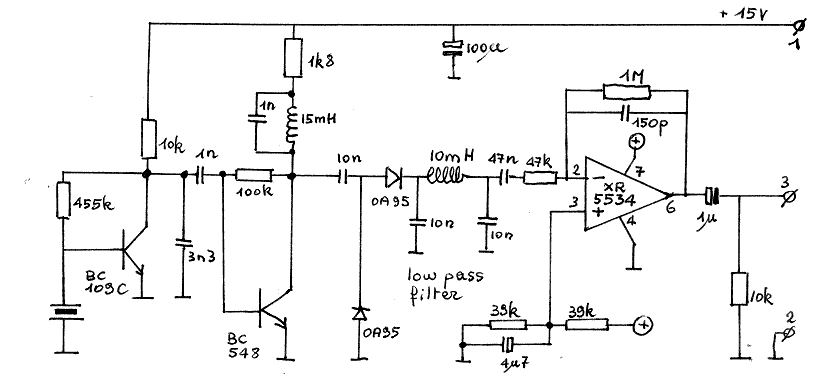
De globale schakeling reageert bijzonder gevoelig op bewegingen maar is geplaagd door een aantal manifeste nadelen:
- de nog steeds betrekkelijk grote achtergrondruis.
| Het beste rezultaat dat we qua signaal-ruisverhouding ooit met dit type AM-detektors konden behalen was 46.5dB (meting uitgevoerd via aflezing der waarden op het oscilloskoopscherm). Dit voor een ontvanger gebouwd voor 50kHz en een (kwazi) ruisvrij zendersignaal uiteraard. Dit rezultaat is echter niet volledig relevant voor muzikale toepassingen, aangezien we de metingen uitvoerden met een gestandaardizeerde afstand tussen zender en ontvanger van 1 meter. Het rezultaat met praktijkafstanden van 3 tot 8 meter tussen zender en ontvangers is vanzelfsprekend aanzienlijk slechter. |
- de gevoeligheid daalt kwadratisch met de afstand van de beweger (het lichaam) tot de ontvanger. De amplitude van de verschiltonen is met andere woorden niet uitsluitend een funktie van de hoeveelheid lichaamsbeweging, maar ook van de plaats ten opzichte van de ontvanger. Dit was duidelijk een ongewenst effekt. Pas in de later ontwikkelde schakelingen waarbij van analoge komputers wordt gebruik gemaakt, wisten we dit probleem op bevredigende wijze weg te werken.
2.3.2.6.2.: Phase Locked Loops
Ontevreden over de vrij slechte signaal-ruisverhouding van de door bovenstaande schakeling haalbare signaal-ruisverhouding, hebben we dan andere metodes van demodulatie uitgeprobeerd. Zo onder meer door toepassing van de 'phase-locked-loop'.
Het beste rezultaat dat we onder toepassing van het PLL-principe konden bereiken, was met onderstaande praktische schakeling:
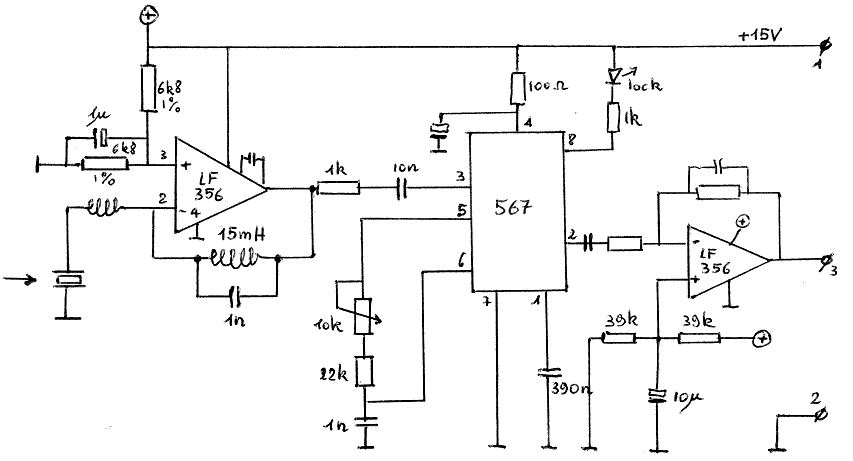
Het muzikale rezultaat was echter meer dan ontgoochelend. Hoewel de signaal-ruisverhouding nu inderdaad stukken beter was, kregen we nu te maken met explosieve geluiden afkomstig van het aan-en-af schakelen van de 'loop-lock'. Bovendien klonken de verkregen tonen nu helemaal syntetisch, zo'n beetje in de zin van de elektronische muziek uit de jaren '50... Dit is natuurlijk een gevolg van het feit dat bij deze schakeling de rezulterende audiofrekwenties opgewekt worden door een spanningsgestuurde oscillator (VCO) in de PLL-chip.
Later kwamen we erachter dat dit ook de principiele techniek was die Wolf-Dieter Trüstedt tussen 1974-1976 uitgeprobeerd had voor zijn bewegingshologrammen, die we wel reeds kenden sedert 1977 en waarvan we ons de slechte rezultaten op het vlak van de haalbare signaal-ruisverhouding konden herinneren.
| Een gedetailleerde beschrijving van het systeem opgezet door Wolf Dieter Trüstedt voegden we toe in de appendix bij deze studie. Een geluidsopname van de door Trüstedt in 1977 behaalde rezultaten bevindt zich in het klankarchief van Stichting Logos te Gent. |
2.3.2.6.3: FM-demodulatie: Foster-Seeley schakeling
De experimentele rezultaten evenals de teoretische studie die erbij tepas kwam, stuwde ons als het ware in de richting van schakelingen voor frekwentie-demodulatie. Op teoretische gronden kon immers door FM-demodulatie toe te passen, meer van de snelheidsinformatie uit de bewegingen teruggewonnen worden. Bij AM-schakelingen waren vooral de amplitude-variaties dominant. Dit ondanks het feit dat de signalen waarmee we hier te maken hebben eigenlijk helemaal geen FM-gemoduleerde signalen zijn, maar integendeel een permanente som van signalen met frekwenties gelegen tussen de draaggolffrekwentie en de Doppler-frekwentie veroorzaakt door het snelste punt van het bewegend lichaam [ fc + (2 * fc * vgeluid) / Vobjekt]. Een mengsel van golven dus, of een kleur-ruisband. Bovendien is ook bekend dat FM-techniek principieel veel betere signaal-ruisverhoudingen kan realizeren dan AM, reden waarom men voor radio-omroepgebruik ook van de ene naar de andere techniek overstapte.
De toepassing van frekwentiedemodulatie voor de frekwentiegebieden waarmee we hier bezig waren, kent evenwel weinig toepassingsvoorbeelden in de klassieke tekstboeken met betrekking tot elektronika. Daarom zijn we uitgegaan van enkele klassieke schakelingen uit de radio-techniek en hebben we die herberekend voor gebruik binnen ons bereik. Het eerste praktisch probleem was dat de spoelen die voor dergelijke schakelingen noodzakelijk zijn, niet in de handel zijn te verkrijgen. Zelf wikkelen was dus de boodschap... Het rezultaat van een dergelijke onderneming zal iedereen die met elektronika vertrouwd is wel goed bekend zijn: de praktijk en de berekening gaan op een onvoorspelbare wijze uiteen lopen, dit omwille van de talloze onbekenden bij het maken van spoelen. Van alle elektronische komponenten is de spoel immers die komponent die in zijn technische realizatie het verst durft afwijken van zijn wiskundig model.
| Het onderwerp wordt zeer uitvoerig behandeld in "The ARRL Handbook" , een imposante jaarlijkse publikatie (meer dan 1000 paginas) van de "American Radio Relay League", (Uitgave 1989), p.18.1 tot p.18.25 en p.9.1 tot p. 9.13. Beknopter kan de modulatie en demodulatie teorie ook aangetroffen worden in Horowitz & Hill, "The Art of Electronics" , 1980, p.567-579 Een ook wiskundig vrij extensieve uiteenzetting over het onderwerp is aan te treffen in :Fink & Christiansen (Red.), "lectronics Enegineers' Handbook" , daarin meer bepaald het hoofdstuk 'Modulators, demodulators and converters' van Chovan, J.L , Egtvedt, M.D. e.a. , Sektie 14, p.1-72. |
De eerste bruikbare schakeling die we vanuit dit perspektief aan een onderzoek op bruikbaarheid onderwierpen was de zgn. Foster-Seeley schakeling. Wat ons intrigeerde in het opzet van dit type demodulator was het in de literatuur vermelde gegeven dat wanneer het op de ingang van een Foster-Seeley schakeling ter demodulatie aangeboden signaal niet in dynamiek werd gelimiteerd, de schakeling gevoelig was voor AM-modulatie in het ingangssignaal. (Dit in tegenstelling tot de verhoudingsdetektor ('ratio-detector') waarover we het verder nog zullen hebben en waarvoor dit in veel mindere mate geldt.)
| Cfr.GAWLER, G.B. "Frequency Converters and Detectors" in: Fink & Christiansen, op.cit., p.14-70. |
Voor 'normale' toepassingen (FM-radio dus) moet dit inderdaad wel een euvel wezen, maar wij zagen er een mogelijkheid in om voor ons doel eigenlijk twee vliegen in een klap te vangen: het behoud van de amplitude-modulatie komponenten uit het ingangssignaal in het audiorezultaat samen met het winnen van de frekwentie-modulatiekomponenten ervan. Onze toch op enige analyze berustende intuitie ging er immers van uit dat in het holosound systeem, de grootte van het bewegend oppervlak alleen kon worden teruggevonden in de amplitude van het totale gereflekteerde signaal, terwijl de snelheids-informatie alleen in de breedte van de ruisband besloten kon liggen.
De schakeling van Foster & Seeley berust op een gestemde hoogfrekwent transformator waarbij de diode aan de ene tak van de wikkeling de piek-waarde van (V1+V2) / 2 detekteert, terwijl de diode in de andere tak de piek-waarde van (V1-V2) / 2 detekteert. Het audio-signaal is niets anders dan het verschil tussen beide. Wanneer een inkomende frekwentie overeenstemt met het centrum van de frekwentie waarop de spoeltransformator werd afgestemd, dan is dit verschil gelijk aan nul. Er was geen te moduleren signaal, alleen een draaggolf. Afwijkingen in frekwentie naar onder toe, doen de spanning in de onderste tak afnemen en die in de bovenste toenemen. Dit heeft een positief signaal op de uitgang voor gevolg. Analoog redenerend, rezulteert dan een frekwentieafwijking naar boven toe, in een negatief signaal op de uitgang. Kortom, we krijgen de modulatie-komponent van het FM-signaal terug in de oorspronkelijke vorm.
Vanuit het principiele schema uit het teorieboek:
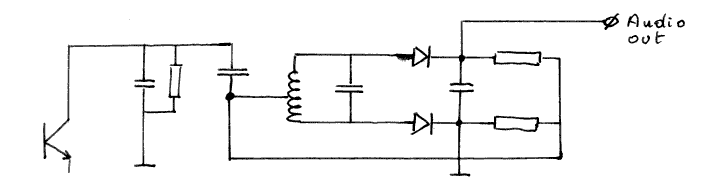
ontwikkelden we na veel geëxperimenteer met spoelen, volgende goed werkende schakeling. Op te merken valt, dat dit ontwerp in tegenstelling tot veel van onze vroegere ontwerpen, relatief gemakkelijk verstembaar kan worden uitgevoerd. Alleen de kring rond de sekondaire wikkeling van de spoeltransformator dient op resonantie te worden gedimensioneerd. Ook bleek het nuttig de Q-faktor van de spoel aan de lage kant te houden, aangezien dit de bandbreedte ten goede komt. Anders dan bij radio-ontwerpen geldt een grote selektiviteit hier immers niet als een kwalitatieve vereiste.
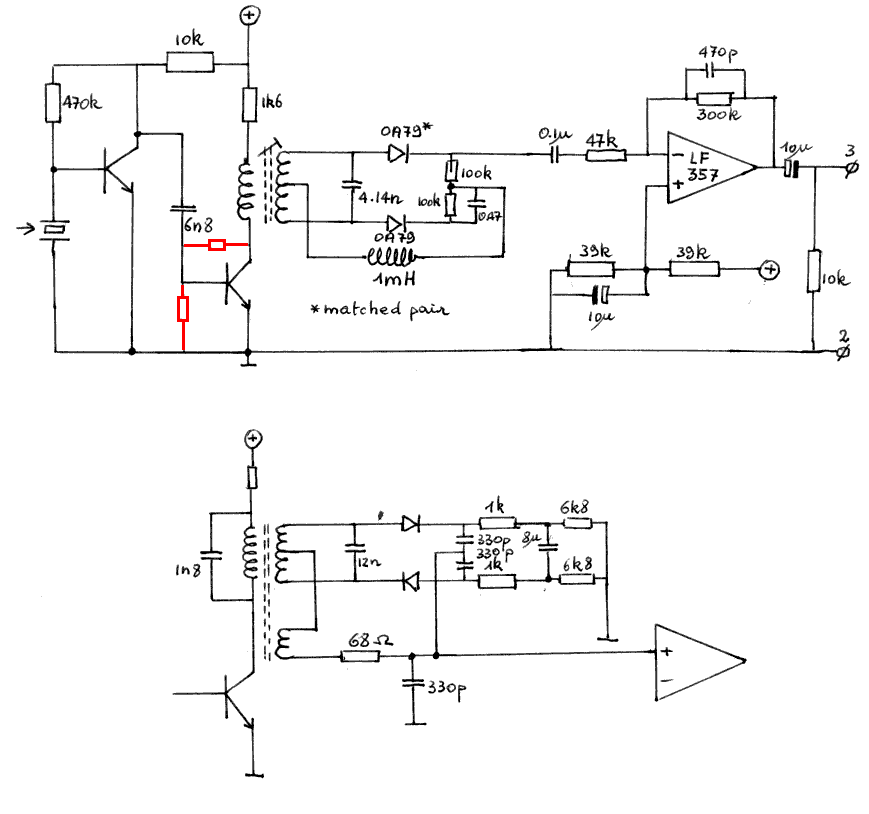
Het gedeelte van bovenstaand schema dat onderaan in een gewijzigde vorm staat getekend, is een werkend ontwerp van een ratio-diskriminator schakeling, in zekere zin een variant op de klassieke Foster-Seeley schakeling. Deze schakeling levert nog meer snelheidsafhankelijke informatie in het rezulterend audio-signaal en is (zoals tevoren reeds opgemerkt) ook minder gevoelig voor amplitudevariatie van het ingangssignaal. Dit laatste uiteraard binnen bepaalde grenzen, want ook deze schakeling doet in de praktijk wel degelijk ook wat aan AM-demodulatie.
De teorie-boek schakeling (op.cit. p.14-70) waaruit we haar ontwikkelden ziet eruit alsvolgt: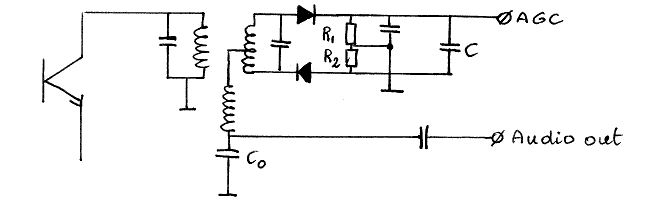
Deze schakeling doet beroep op een spoel met een extra wikkeling en is dan ook aanzienlijk moeilijker te bouwen. De mate van ongevoeligheid voor AM-modulatie in het ingangssignaal hangt af van de tijdkonstante (R1+R2) * C die groot dient te zijn in verhouding tot de laagste frekwentie die men wil behouden in het uitgangssignaal. De kondensator Co dient het draaggolfsignaal kort te sluiten, maar moet een zo gering mogelijke weerstand vormen voor het te winnen audio-signaal. Het zal duidelijk zijn dat dit in onze toepassing niet echt optimaal mogelijk is, aangezien de draaggolfrekwentie in deze ultrasone toepassingen niet zo heel erg ver verwijderd is van het audio-gebied dat ons interesseert!
2.3.2.6.4: Hoogfrekwent-voorversterker
De toepassing van de op de Foster-Seeley schakeling gesteunde ontwerpen betekende een grote stap voorwaarts op kwalitatief vlak. Maar aangezien in elke denkbare wereld alles steeds voor verbetering vatbaar is, zochten we verder tot we op het idee kwamen een analoge komputer in te zetten voor het hele demodulatiegebeuren.
Dit vereenvoudigde de ontwerptechnische eisen van het ontvanger-gedeelte meteen aanzienlijk. Nu kon immers volstaan worden met een front-end waarin het ontvangen signaal, ongewijzigd maar hooguit beperkt in de dynamiek via een eenvoudige kompressor-schakeling, op een 0dBV niveau werd gebracht.
De thans (1988/93) gebruikte ontvanger-schakeling met optimale rezultaten ziet er uit alsvolgt:
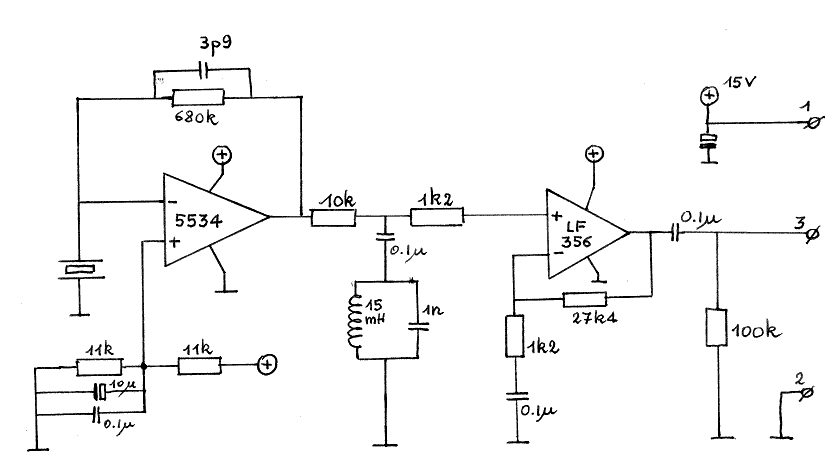
De eerste trap, die een spanningswinst oplevert van ca.40dB, heeft als enige eigenaardigheid, dat de transducer (een piezo-exemplaar in dit geval) zonder enige voorschakelweerstand aan de inverterende ingang van de opamp komt te liggen. Deze laatste werkt dan ook als stroomversterker, terwijl de transducer virtueel kortgesloten wordt. Deze konfiguratie bleek de beste lineariteit op te leveren voor de transducer, ten koste van wat signaalverlies weliswaar. Alle resonantiepieken die op het nivoo van de transducer ontstaan wanneer de ontvangst van het draaggolfsignaal sterk in amplitude gaat schommelen, worden hierdoor uitgevlakt. De bandbreedte wordt gemaksimalizeerd. De LC-resonantiekring die op de eerste op-amp volgt is optioneel, en wordt alleen gebruikt in toepassingen met een vaste zenderfrekwentie in welks geval de kring wordt afgestemd op de betreffende frekwentie. De Q-faktor mag evenwel niet te groot genomen worden, want dan wordt de spanning op de ingang van de volgende trap te groot en treedt er clipping op. De eindtrap, eveneens een operationele versterker, is gedimensioneerd voor een spanningswinst van 27dB. De over-all versterking van de schakeling beloopt 2280 maal. De nominale uitgangsspanning is 0dB. In gebalanceerde toepassingen wordt de laatste trap als een aktieve symmetrische driver uitgevoerd met behulp van een dubbele opamp, ofwel wordt aan de laatste trap een miniatuur audio-transformator toegevoegd. Gezien de hoge frekwentie kan ook een ferrietpotkerntransformator gebruikt worden voor dit doel.
Deze schakeling doet in tegenstelling tot alle vroegere ontwerpen dus helemaal niets aan de demodulatie. Het signaal komt eruit zoals het erin ging, alleen 2280 maal sterker. Ze heeft dus ook geen enkel hoorbaar rezultaat!
Een volstrekt lineaire schakeling die we gebruikten voor ultrasone ontvangers gebruik makend van (Murata) piezo-transducers in het 200kHz bereik, maar die evengoed bruikbaar is voor eender welke ultrasone frekwentie, werd opgebouwd alsvolgt:
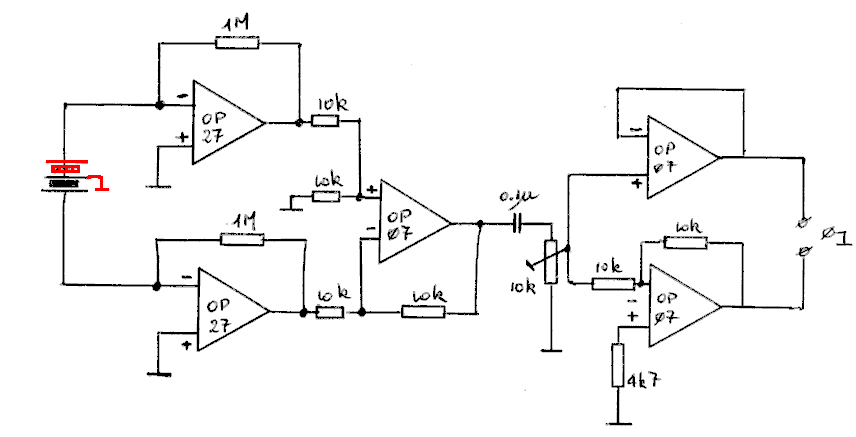
2.3.3.: De analoge komputer: demodulatie-schakelingen
2.3.3.1: Multipliers
Geïnspireerd door een aantal schakelingen uit de hoogfrekwent-techniek, waarbij voor de demodulatie de draaggolf gescheiden van het gemoduleerde signaal dient toegevoerd te worden (single-side-band modulatie bvb.), zijn we na de suksessen met de frekwentiedemodulatieschakelingen, in deze richting verder gaan zoeken. Immers door iets dergelijks met onze signalen toe te passen, was het mogelijk de draaggolf van het ontvangen signaal integraal af te trekken en zodoende uitsluitend de door de beweger veroorzaakte Doppler-signalen over te houden. Talloze schakelingen die iets dergelijks doen hebben we voor ons doel aangepast en berekend, opgebouwd en vervolgens uitgetest. De rezultaten kwamen niet uit boven de eerder besproken Foster-Seeley schakeling, of indien ze wel degelijk beter presteerden, hadden ze een uiterst miniem dynamisch bereik zodat ze toch weer geen echt valabel alternatief boden.
Bij een gescheiden behandeling van draaggolf en gemoduleerd signaal hadden we twee mogelijke wegen te bewandelen:
- het was mogelijk via een selektief LC-filter (een parallel geschakelde kring bestaande uit een spoel en een kondensator) of iets dergelijks de draaggolf vrij goed te izoleren uit het ontvangen signaal. In de radiotechniek is dit rekonstitueren van de draaggolf een standaardprocedure bij de demodulatie van o.m. SSB-signalen.
- aangezien onze toepassing evenwel niets met draadloze transmissie of kommunikatietechniek te maken had, beschikten we over de mogelijkheid het draaggolf signaal rechtstreeks in elektrische vorm van de zender, waar het tenslotte zijn oorsprong vond af te leiden. Demodulatie kon dus eigenlijk ook plaatsvinden uitgaande van het zendersignaal zelf en de drie ontvangersignalen. Het enige -en zoals uit de experimenten later bleek in hoge mate teoretische- probleem met een dergelijke procedure, is dat van de tijdsvertraging tussen audio-transmissie enerzijds (bepaald door de afstand tussen zender en ontvanger in kombinatie met de geluidssnelheid) en de snelheid van elektrische signalen via de elektrische geleiders anderzijds (quasi uitsluitend bepaald door de snelheid van het licht).
| Uit een nauwkeurige meting blijkt immers dat ook de draagolf zoals zij zelfs wanneer er helemaal geen beweging binnen het bestreken veld plaatvindt, niet als een zuiver sinusvormig signaal bij de ontvanger terechtkomt. Integendeel, kunnen we deze golf met talloze fazeverschuivingen aantreffen in het ontvangen signaal, dat eigenlijk alleen een rekenkundige som is van alle in faze allesbehalve zo koherente ontvangen draaggolfrekwenties. Deze inkoherenties treden evenwel niet op in het akoestische 'open veld', maar wel vanzodra de proeven in een met wanden besloten gebouw plaatsvinden. Zij uiten zich -bekeken op het scherm van een oscilloskoop niet zozeer als een bundel sinussen, maar wel in de vaststelling dat de ontvangen signaalsterkte, in acht genomen een voldoend grote afstand tussen zender en ontvanger, op anders onverklaarbare wijze toe- en afneemt wanneer we de ontvanger slechts enkele frakties van een golflengte verplaatsen. |
Toen herinnerden we ons een toestel waarmee we reeds in 1968-1969 vrij veel hadden gewerkt en wel in verband met elektronische muziek: de ringmodulator. In oorsprong eigenlijk ook wel een schakeling afkomstig uit de hoogfrekwente techniek, maar dan een die via de telefonie ook in het audio-gebied aanwendingen had gevonden.
De 'klassieke' ringmodulator is een schakeling met twee ingangen en één uitgang die zich zo gedraagt dat wanneer op de twee ingangen signalen f1 en f2 aangeboden worden, de uitgang alleen de som- en verschilfrekwenties tussen f1 en f2 en hun veelvouden laat verschijnen, terwijl zowel f1 als f22 zelf volledig worden opgeheven. Zo'n klassieke ringmodulator, in deze tijd reeds een museumstuk, ziet er schakeltechnisch uit alsvolgt:
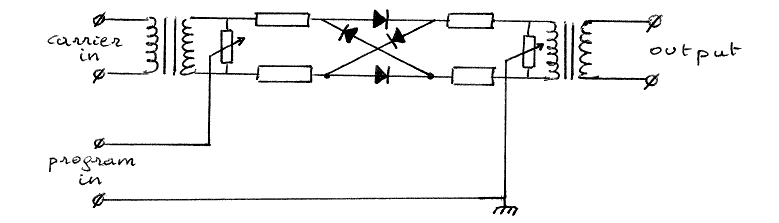
Cfr.:BODE, Harald & MOOG, Robert "The Multiplier-Type Ring Modulator", in: Electronic Music Review, january 1967.p.9-15.
Toegepast op onze probleemstelling, zou een dergelijke schakeling dus enerzijds alle som-frekwenties tussen draaggolf en ontvangersignaal, en alle verschilfrekwenties daartussen opleveren. In de som zijn we niet geinteresseerd. Haar kunnen we via een low-pass filter gemakkelijk kwijtspelen. Het verschilsignaal, is niets minder dan het gewenste uitsluitend van de beweging afhankelijke geluidssignaal waaruit de draaggolf is verdwenen.
De problemen verbonden met een goed praktisch ontwerp van zo' schakeling zijn echter -zoals we wisten uit onze ervaring ermee uit de periode 1967-1970- aanzienlijk. De eisen te stellen aan de kwaliteit van de transformatoren (symmetrie en onderlinge identiteit) en aan de diodes (onderlinge identiteit, ook qua temperatuurkoëfficient) waren zo groot, dat de praktische schakeling steeds leed aan sterke vervorming en een flink doorlekken van de ingangssignalen naar het uitgangssignaal. De praktijk stond dus ver af van de teorie.
Zoekend naar meer eigentijdse uitvoeringsmogelijkheden van een naar werking gelijkaardige schakeling, werd onze aandacht getrokken naar de diverse 'balanced-modulator-demodulator' chips die door verschillende fabrikanten aangeboden werden. Dit zijn schakelingen waarvan het wiskundig model heel trouw overeenkomt met dat van de eerder vermelde ringmodulator, en waarmee dus in principe hetzelfde rezultaat te bereiken valt.
Volgende gebalanceerde demodulators in chipvorm onderwierpen we aan een grondig onderzoek, telkens door konform de specifikaties en de application notes, een testschakeling in funktie van ons doel op te bouwen, uit te meten en te evalueren:
- Philips TDA0820T, MC1496, MC1596
of National Semiconductor, LM1496N,LM1596
Signetics S5596
Motorola MC1496P
Intersil ICL8013
Harris HA2546, HA2547
Van al deze chips, gaf de LM1496 in onze toepassing de beste rezultaten. Deze schakeling gaan we dan ook iets uitvoeriger toelichten.
2.3.3.2: De LM1496 schakeling
Ingangsspanningen mogen niet veel groter worden dan ca. 150mVtt voor een onderdrukking van de ingang rond 50dB. De gelijkstroominstelling van de chip is bijzonder kritisch.
Deze chip is intern opgebouwd als een kombinatie van spanningsgestuurde stroombronnen. Het hier sterk vereenvoudigd weergegeven interne schema van de opbouw van de chip brengt dit heel duidelijk aan het licht:
| Cfr.: Philips, Databook 8, May 1982, "Analogue Circuits", p.14-17.(databoek) |
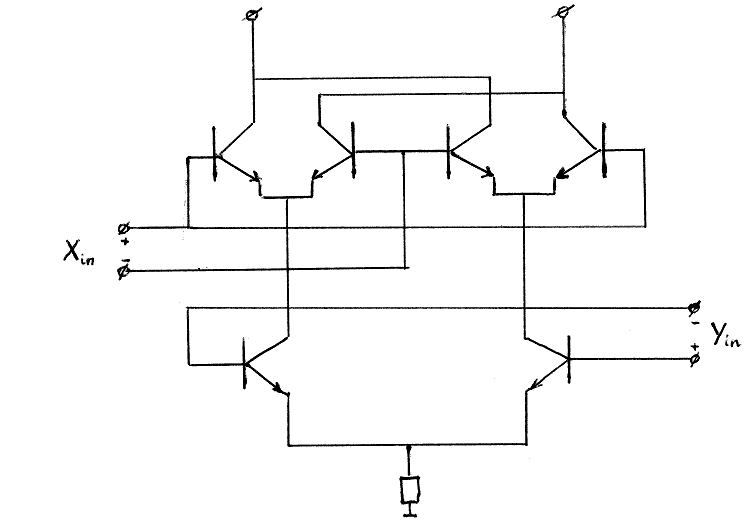
De volledige schakeling, hoewel we ze toch enkele jaren met sukses voor publieke opvoeringen van het 'Holosound' muziekteaterstuk hebben gebruikt, was bijzonder gevoelig voor asymmetrieën in de voedingsspanningen. Via trimmers op de print kon de asymmetrie weliswaar weggeregeld worden, maar dit diende kwazi permanent te gebeuren, een omstandigheid die voor praktische toepassingen in een muziekinstrument dat ook door niet technisch geschoolden bruikbaar zou zijn uiteraard hoogst bezwaarlijk was. Het probleem kon op het nivoo van de voeding niet zomaar worden opgelost. De precizie van deze laatste, qua dynamische tracking, hadden we reeds tot 0.1% opgedreven, toch dicht aan de grens van wat volgens de diverse tekstboeken terzake en zonder astronomische kosten, haalbaar is.
Een groot voordeel van de schakeling is dat ze ongewijzigd kan worden gebruikt in kombinatie met alle ultrasone zendfrekwenties.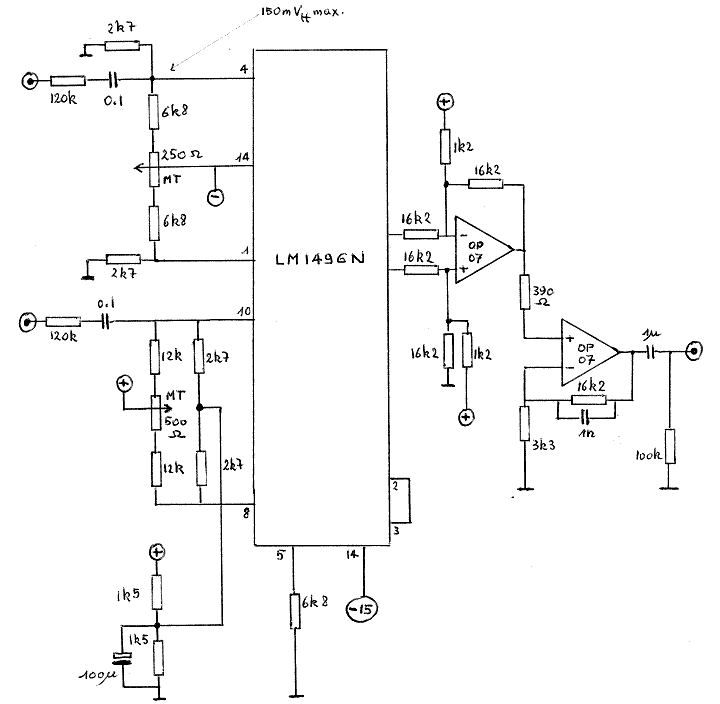
2.3.3.3: De analoge komputer
Op een klaarblijkelijk goed spoor gezet door de vorige schakeling, belandden we uiteindelijk bij het idee een meer universele demodulatieschakeling te gaan inzetten. Daarbij kwam dan het algemene koncept van de analoge komputer voor de hand te liggen. Immers de gebalanceerde modulatorschakeling is uiteindelijk slechts een bijzondere toepassing van wat meer algemeen gesproken een vierkwadrantvermenigvuldiger genoemd wordt. 'Vierkwadrant' slaat er hier op dat het teken van de ingangsspanningen zowel positief als negatief mag zijn waarbij dan uiteraard de schakeling toch steeds een korrekte vermenigvuldiging zal uitvoeren.
In algemene zin is elke elektronische schakeling die n kontinu variabele ingangssignalen via een definieerbare overdrachtfunktie omzet in een kontinu variabel uitgangssignaal, een analoge komputer. De wellicht meest voor de hand liggende als analoge komputer bruikbare schakeling -overigens ook een van de meest gebruikte schakelingen in de analoge elektronika- is de operationele versterker:
| Ook de 'gewone' vermogensgeluidsversterker is te beschouwen als een analoge komputer: hij vermenigvuldigt de amplitude van een ingangssignaal met een instelbare konstante faktor volgens de eenvoudige betrekking Uo * Io = (Ui * Ii) * Av |
Wanneer we in deze algemene schakeling van een zogenaamde verschilversterker de impedanties van z1, z2, z3, z4 als zuiver resistief beschouwen en we bovendien stellen z1 = z2 en z3 = z4 dan wordt de lineaire overdrachtfunktie gegeven door:
- Uo = (z3 / z1) * ( U1 - U2)
Voor sinusvormige signalen verkrijgen we dus de overdrachtfunktie [(sin(a) - sin(b)) * z3] / z1 die voor a = b dus geen signaal oplevert, wat, in audio-termen uitgedrukt, betekent dat signalen die identisch op beide ingangen tegelijkertijd verschijnen (zelfde frekwentie, zelfde amplitude, zelfde golfvorm en zelfde faze), niet in het uitgangssignaal aanwezig kunnen zijn. Hierop berust het gebruik van deze schakeling voor de storingsonderdrukking bij signaaloverbrengingen (o.m. mikrofoon-aansluitingen e.d.m.). Storingen die van buitenaf een elektrische kabel binnendringen, doen dat immers met beide signaalgeleiders in gelijke mate. Het storingssignaal voldoet dus in grote mate aan de hiervoor gestelde voorwaarde om opgeheven te worden. In technische termen noemt men dit 'ommon mode rejection'.
Door -rekening houdend met een aantal beperkigen (eindigheden) van de schakeling weliswaar- de impedanties z1 tot z4 komplex en niet-lineair uit te voeren, kan een behoorlijk groot aantal vrij ingewikkelde wiskundige funkties worden geimplementeerd: naast optellen, aftrekken, vermenigvuldigen, en delen ook integreren, differentieren, logaritmen... Aan de teorie zowel als de praktijk van dit soort schakelingen zijn talloze handboeken en teoretische studies gewijd.
We vermelden deze analoge komputer hier, omdat we er verder in deze studie nog uitvoerig gebruik zullen van maken, meer bepaald daar waar we gesteld voor de keuze tussen digitale en analoge signaalverwerking, uiteindelijk voor de analoge weg hebben gekozen. We menen bovendien te kunnen aantonen dat het ook, hic et nunc, de beste keuze was.
Een aantal fabrikanten van elektronische komponenten heeft zich specifiek toegelegd op meer komplexe schakelingen voor gebruik als analoge komputer. Zo onder meer het Amerikaanse Analog Devices. Van dit bedrijf kochten we een stel chips, type AD632: een precisie vierkwadrant vermenigvuldiger. Deze schakeling biedt een bijzonder goede signaal-ruisverhouding (90µVrms in de frekwentieband van 10Hz tot 10kHz) en haalt zelfs zonder externe afregeling ('trimmen') een precisie van 0.5% op het rezultaat van de overdrachtfunktie als vermenigvuldiger. Bovendien is ze eveneens geschikt om -mits enkele kleine wijzigingen in de externe bedrading- te worden gebruikt als deler, machtsverheffer en worteltrekker. De eenvoudig te realizeren overdrachtfunkties zijn:
- vermenigvuldiger:- Uo= [(X1 - X2) * (Y1 - Y2) / 10]+ Z2
- {[sin(a) * sin(b)] / 10} + sin(c)
= {[cos(a-b) - 1/2 cos(a+b)] / 20} + sin(c)
De analoge vermenigvuldiger heeft een procentuele fout van 0.5%, of, -met het oog op hoofdstuk 3, een (bijna) 8-bits rezolutie.
- deler:
- Uo = {[(Z2 - Z1) * 10] / (X1 - X2)} + Y1
Hierbij geldt echter de beperkende konditie: X1 > X2, ook hier is delen door 0 immers ontoelaatbaar. De analoge deling wordt uitgevoerd met een procentuele fout van 0."75%", of, een rezolutie van 7-bits.
- kwadrateerder:
- Uo = {[(X1 - X2)2] / 10} + Z2
- worteltrekker:
- Uo = {[(Z2-Z1) * 10] ^ (1/2)} + X2
en dit met procentuele fout <=1%, (7-bits rezolutie).
Met slechts enkele extra onderdelen kunnen verder nog volgende funkties gemakkelijk worden gerealizeerd:
- verschil van de kwadraten
- Uo = [(X^2) - (Y^2)] / 10V
- Uo = -1V * Log10(Z / X)
(de exponent mag daarbij zelfs een real-time variabele zijn)
- Uo = Y * [(Z/Vref)^m] V
- UΘ = (UΘref - UΘ) * [(Z / X)^1.21]
waarbij Θ = Tan-1(Z/X)
| Cfr.: Analog Devices, Linear Products Databook, p.6.3-6.47 |
Opgemerkt moet worden, dat alle formules slechts gelden voorzover de a priori grenzen van de in- en uitgangssignalen niet worden overschreden. Voor beide, dienen deze zich te beperken tot het trajekt -10 tot +10Volt, wanneer de chip wordt gevoed uit een symmetrische +/-15Volt voeding. Ook aan de snelheidsveranderingen van de ingangssignalen zijn grenzen gesteld (voor periodieke signalen dus aan hun frekwentie), maar deze zijn voor ons doel nauwelijks van enige betekenis. De chip-specifikaties laten voor de voor laagfrekwente toepassingen geoptimalizeerde AD632 signaalfrekwenties toe tot 1MHz. Dit soort schakelingen is zelfs voor frekwenties van 50MHz (AD539) en veel hoger (de AD834 bvb. voor 500MHz) beschikbaar, iets waar geen enkele digitale implementatie zelfs maar kan van dromen.
De schakeling die we gebruik makend van deze komponent realizeerden werd een werkelijke real-time analoge rekeneenheid, samengesteld uit verschillende rekenkundige blokken. Elk blokje van de blokkendoos heeft een of twee symmetrische (gebalanceerde) ingangen en één symmetrische uitgang. Van elk blok zijn er telkens drie identieke exemplaren voorhanden in de blokkendoos, terwijl elk verschillend blokje een andere wiskundige overdrachtfunktie kan uitvoeren. De blokkendoos omvat verder nog een 3-kanaals limiter/compressor, een drie-kanaals filter en een lijnversterker/buffer waarmee de modulair opbouwbare schakeling wordt afgesloten.
Laten we elk blok van dit analoog-komputerontwerp aan een gedetailleerd onderzoek onderwerpen:
2.3.3.3.1 Ingangstrap:
De ingangsschakeling bestaat uit driemaal het bovenste gedeelte van de hierbij afgebeelde schakeling en eenmaal het onderste stuk. Het VU-meter gedeelte komt viermaal voor. Op de drie identieke ingangen worden de uitgangen van de ontvangerschakeling aangesloten. De onderste ingang krijgt het signaal van de ultrasoonzender direkt aangeboden. Deze ingang is asymmetrisch uitgevoerd omdat alle door ons ontworpen zenders dit signaal ook zo afgeven en omdat dit signaal, gezien het de draaggolf zelf is, een konstante amplitude heeft. Na een gewone buffer wordt het signaal gesplitst. Eén tak gaat via een potentiometer naar een versterkertrapje en zo naar de uitgang. De andere tak gaat naar een als nul-doorgangsdetektor geschakelde komparator (LM311). Deze levert bij elke nul-doorgang van het draaggolfsignaal een puls af. Deze mogelijkheid werd vooral ingebouwd om een aantal bijzondere experimenten mogelijk te maken. De frekwentie van deze pulsen is nu immers de dubbele draaggolffrekwentie. Met de potentiometers van de tak naar keuze (daarom de wisselschakelaar) wordt het draaggolfsignaal in balans gebracht met het signaalnivoo van de X,,Z ingangen.
Het schema voor de X,,Z ingangen (bovenste helft) is een klassieke instrumentatieversterker en dus geschikt voor het aansluiten van symmetrische ingangssignalen. Voor asymetrische signalen wordt een van beide ingangen (maar wel voor alle drie kanalen dezelfde) aan massa gelegd. Met de 50kΩ potentiometer kunnen de kanalen worden uitgebalanceerd. In principe verstoort elke regeling de precizie van de later uitgevoerde rekenkundige bewerkingen op de signalen. Wanneer de opstelling in het akoestisch vrije veld wordt gebruikt is ze niet alleen volkomen overbodig, maar bovendien ook storend. Daarom werd de potmeter uitgevoerd als een gekalibreerde stappenschakelaar met metaalfilmweerstanden. In praktische (koncert)ruimtes verstoren architekturale asymmetrie en sekondaire reflekties van wanden en meubilair vaak het evenwicht tussen de drie kanalen. In dergelijke gevallen is een afregeling wel noodzakelijk. Om dit mogelijk te maken werd de schakeling uitgerust met 4 kleine VU-metertjes waarop het geintegreerd signaalnivoo kan worden afgelezen. De trimmer laat toe het schaalbereik aan het gebruikte meetinstrumentje aan te passen.
De schakeling is zo gedimensioneerd dat de uitgangen binnen het spanningsbereik +/- 10V vallen.
| Gebruikte data-boeken: National Semiconductor, "Linear Databook, vol.1", (1988), p.4.18-4.30 (komparatorschakeling), Analog Devices, "Linear Products Databook", (1988), p.2.223 - 2.236 (Op-amp schakelingen met OP07 en OP27). In een recentere versie van deze schakeling hebben we gebruik gemaakt van de pas onlangs op de markt gebrachte dubbele opamp OP227, wat heel wat printplaatoppervlak uitspaart. |
De bovenste helft wordt driemaal identiek opgebouwd.
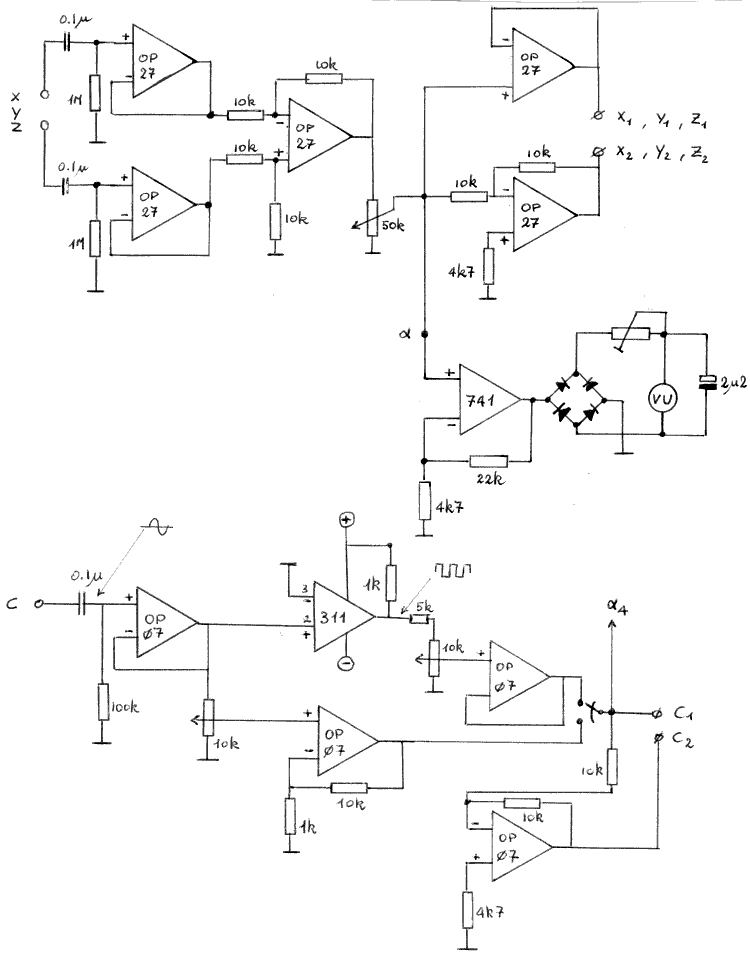
2.3.3.3.2: Analoog rekenblok voor vermenigvuldiging
Deze schakeling is een rechttoe-rechtaan toepassing van de standaardapplikatie voor de Analog Devices multiplier AD632. De pin-nummers slaan op de TO100 verpakking (rond metalen huisje) omdat we de chips in die verpakking geleverd kregen. Een 14pin DIL verpakking zou ook leverbaar moeten zijn en kan het printontwerp iets eenvoudiger maken.
Deze vermenigvuldiger hebben we eveneens opgebouwd gebruik makend van de -goedkopere- AD532 (goedkoop, alhoewel de chip in 1990 en in Gent toch ook nog steeds zo' 3.200 BF per stuk kostte...). De verschillen in prestatie zijn weliswaar meetbaar, maar auditief vallen ze niet zo erg op. De precisie is iets lager (maximaal 1%) maar voldoet nog steeds aan onze (eigenlijk pas verder in dit onderzoek naar voor komende) eis tot 7-bit rezolutie. Een nadeel verbonden aan het gebruik van de AD532 chip is dat er voor een perfekte werking een trimpot gebruikt dient te worden en er dus een afregeling noodzakelijk is.
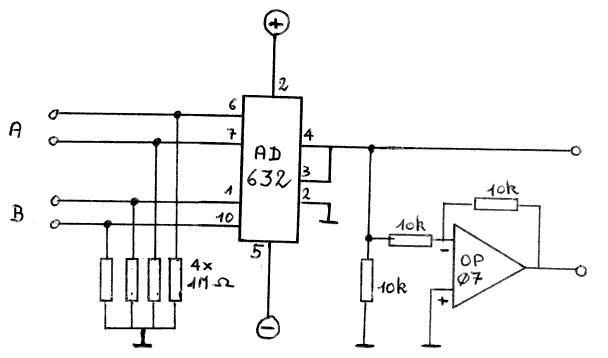
2.3.3.3.3 Analoog rekenblok voor 'verschil der kwadraten'
Ook deze schakeling liet ons weinig ruimte voor ontwerptechnische kreativiteit en is dus een toepassing van de door Analog Devices gesuggereerde schakeling. De operationele versterker dient uitsluitend als faze-draaier (inverter). De twee 20kΩ weerstanden dienen minstens een precisie te hebben van 0.1%, niet zozeer kwa absolute waarde, maar vooral kwa onderlinge identiteit. Trimmers bleken hier geen goede oplossing te bieden omwille van de lage stabiliteit ervan.
Deze schakeling heeft in tegenstelling tot de voorgaande geen gebalanceerde ingangen. Omwille van de kompatibiliteit met de andere rekenblokken, zijn de ongebruikte fazen via een weerstandje met massa verbonden.
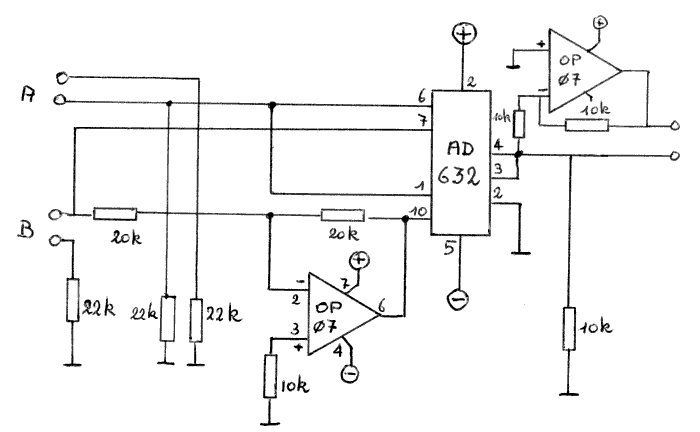
2.3.3.4: Analoog rekenblok voor kwadraten
Deze schakeling geeft, op grond van haar wiskundige overdrachtfunktie, uitsluitend positieve uitgangssignalen (immers, een even macht van een getal is per definitie steeds een positief getal). Willen we negatieve uitgangen, dan dienen we de ingangsaansluitingen te verwisselen. Om de schakeling toch een rond 0V symmetrisch uitgangssignaal te geven, dienen we AC-koppeling toe te passen. Het dynamisch (Uopp) bereik zal echter slechts 10Vtt bedragen en niet 20Vtt zoals bij de andere blokken. Om hieraan te verhelpen, hebben we de uitgang voorzien van een 2x versterker, dit weliswaar ten koste van de DC-koppeling.
De overdrachtfunktie van deze schakeling kan ook eenvoudig bereikt worden met de vermenigvuldiger schakeling, wanneer we deze op beide ingangen hetzelfde signaal aanbieden. De schakeling werd in de analoge elektronische muziek vaak gebruikt voor frekwentieverdubbeling (oktavering) van signalen, of als 'phasor' , waarbij beide ingangen hetzelfde signaal krijgen maar één ingang wordt onderworpen aan een periodieke fazeverschuiving gestuurd door hetzij een extern signaal (LFO) hetzij een vaste interne oscillator.
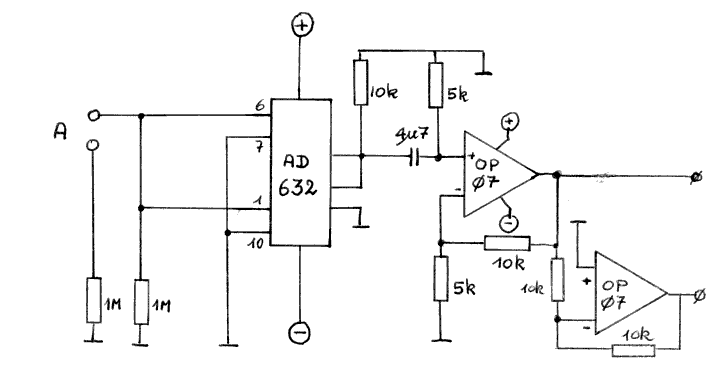
2.3.3.5: Afsluitblok
Dit afsluitblok bestaat uit drie funktioneel verschillende komponenten. Elke komponent is driekanalig (3 x identiek) uitgevoerd. De eerste twee blokken kunnen -door overbrugging van de schakeling- naar believen al dan niet in de signaalweg opgenomen worden. Immers, deze komponenten zijn niet bij alle instelbare overdrachtfunkties nuttig of vereist.
2.3.3.3.5.1 Elementaire limiter/kompressor
Na veel geexperimenteer met zogeheten 'compander' IC's (compressor-expander kombinaties in chip vorm) zijn we spoedig teruggekomen op een bijna voorhistorisch ontwerp afkomstig uit de kortegolfradiotechniek: de diodekompressor.
De meer gesofistikeerde chip-schakelingen hadden zonder uitzondering problemen met zgn. 'pompen', dit als gevolg van de vaak voorkomende uiterst lage frekwenties in onze gedemoduleerde signalen. Tenslotte gaat het hier niet over een signaal dat ook maar ergens een statistische gelijkenis vertoont met dat van modale (in de zin van jan-modaal dan...) muziek. Bovendien introduceerden ze een o.i. ontoelaatbare hoeveelheid extra ruis in het eindsignaal.
Het effekt van deze schakeling is vooral van belang voor de muzikale kwaliteit van het audiosignaal: het filtert te steile signalen weg, doordat het bij de kompressie de hoge frekwenties in hogere mate kortsluit dan de lage. Het reageert ook sneller op hoge frekwenties dan op lage. De dimensionering werd op grond van experimenten bepaald. Eigenlijk verstoort zij de 'wiskundige schoonheid' van de rest van de schakeling. Maar wanneer die wiskundige schoonheid de muzikale in het gedrang brengt, bleken we ons hier dan toch in eerste plaats als muzikus op te stellen...
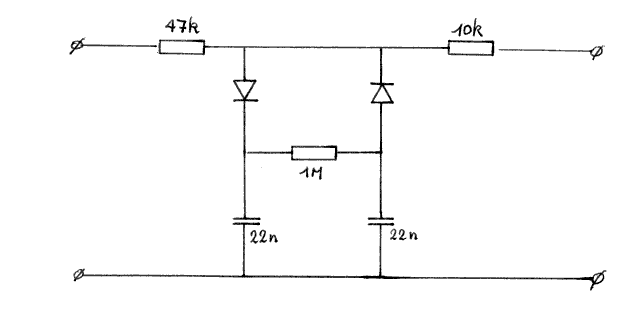
2.3.3.3.5.2 Laagdoorlaatfilter
Dit is een eenvoudig Pi-filtertje opgebouwd met vaste spoelen en MKM kondensatoren. Van de verleiding om ook dit filter als een aktief 'state-variable' aktief filter met operationele versterkers uit te voeren hebben we afgezien, omdat het audio-gedeelte sowieso een vaste bandbreedte heeft in dit ontwerp: van 20Hz tot hooguit zo' 2kHz. Uit een analyze van de frekwentiebanden met een tertsruisfilter bleek er in de banden vanaf zo' 2kHz toch kwazi uitsluitend ruis te steken, en die waren we liever kwijt dan rijk.
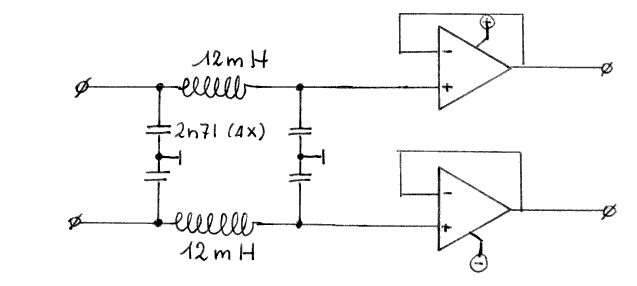
2.3.3.3.5.3 Lijnversterker
De lijnversterker heeft eigenlijk niets bijzonders. De eerste operationele versterker is opgebouwd als verschilversterker met een ingangsimpedantie van 10kΩ. De schakeling werd ontworpen om het signaal tot een gezond audio-signaal te omvormen en daarbij nog een beetje ruis uit het hoog weg te halen. Vandaar het C-tje over de feedback weerstand van de tweede operationele versterker. Het ontwerp is niet helemaal state-of-the-art, want dan hadden we een echte instrumentatieversterker moeten gebruiken. De kosten wogen evenwel niet op tegen de in dit geval uiterst geringe baten.
De uitgang van deze op-amp stuurt een 1:1 audiotransformator. Op deze plek gaven we de voorkeur aan het gebruik van een klassieke transfo omdat het gevaar dat de schakeling zou opgeblazen worden bij aansluiting op een mengpaneel met een fantoomvoeding van 48V ons -gesterkt door ervaring terzake- bijzonder reeel voorkwam. Een tweede niet onbelangrijke reden voor de uitgangstransformator heeft dan weer te maken met het feit dat operationele versterkers nogal eens moeilijkheden ondervinden wanneer ze een sterk kapacitieve belasting aangeboden krijgen. Dit laatste is het geval wanneer lange aansluitkabels gebruikt worden naar het mengpaneel, iets wat in koncertsituaties vrij normaal voorkomt. De waarde van die kapacitieve belasting ontsnapt in principe aan de kontrole van de bouwer, die dus niet in de praktische mogelijkheid verkeert de schakeling hierop te voorzien zoals het technisch hoort. Een transformator is weliswaar ook niet onproblematisch kwa fazegedrag en frekwentiekarakteristiek wanneer hij kapacitief belast wordt, maar tenminste reageert hij niet met een 'fluitjeskoncert' of een rookpluimpje in zulke omstandigheden. Last but not least, een transformator kan zonder problemen ook aan een niet-symmetrische ingang aangesloten worden door een van beide aansluitingen aan massa te leggen, iets wat bij aktief gebalanceerde uitgangen tot kortsluiting aanleiding geeft.
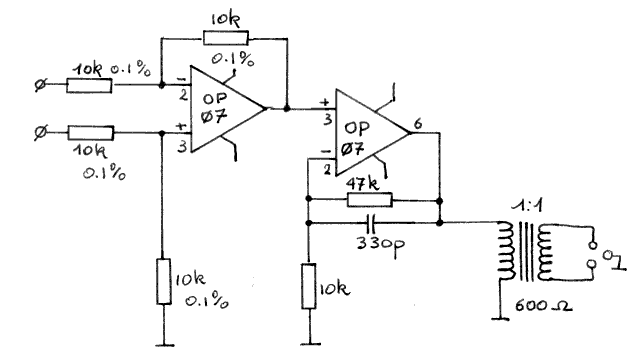
2.3.3.3.6 Voeding...
Dat zo'n schakeling om iets te kunnen verrichten ook van spanning voorzien dient te worden is welhaast zo triviaal dat we daar zelden bij stil blijven staan. Een voeding is nu niet direkt een schakeling waar veel kreativiteit komt bij kijken, zeker niet wanneer ze niet veel meer hoeft te doen dan +15 en -15 volt leveren bij een stroom van hooguit 500mA...
Maar, uit onze proeven is gebleken dat de hier als analoge komputer beschreven schakelingen uiterste eisen stellen aan de kwaliteit van de voeding! Eerst en vooral aan de symmetrie van de positieve en negatieve spanning. De voeding kan dus niet gewoonweg samengesteld worden uit een 7815-7915 kombinatie of iets dergelijks! Bovendien moet de spanning ook een bijzonder laag ruisnivoo hebben en moet zowel de tracking als het dynamisch gedrag uitstekend zijn.
De hiervoor door ons ontworpen tweetrapsschakeling voldoet aan deze eisen. Omdat er niets insteekt dat rechtstreeks en ontwerptechnisch met het eigenlijke onderwerp van deze studie samenhangt, gaan we er ook verder geen bespreking aan wijden.
| Gebruikte bronnen bij het ontwerp: - Horowitz & Hill,"The Art of electronics" , 1981, p.172-218. - National Electronics, "Linear Databook" Volume 1, , 1988, p.1.3 - 1.279. - ARRL Handbook, 1989, p.27.1 -27.26. |
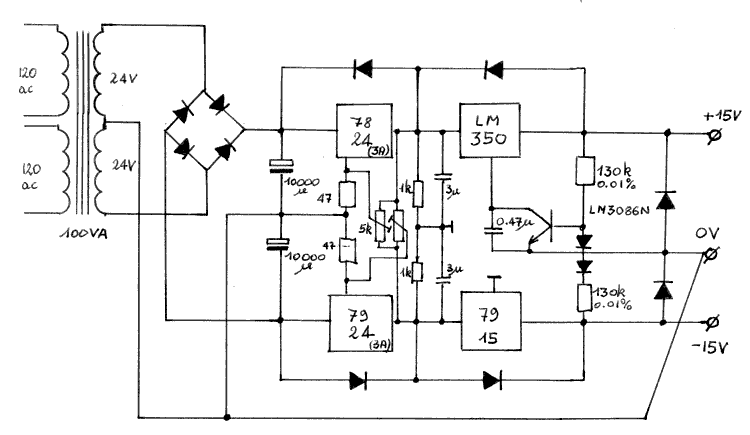
2.3.3.3.7 'Patching'
Ons ontwerp voor een analoge komputer zou geen blokkendoos zijn, indien ze niet op heel wat verschillende wijzen zou kunnen worden samengesteld. Voor het met elkaar verbinden van de verschillende blokken is de Engelse term 'patching' o.i. de meest geschikte. Hij is overigens in de wereld van de elektronische muziek ingeburgerd geraakt in de periode van de analoge synthesizers die via talloze 'patchcords' dienden geprogrammeerd te worden.
Hoewel er tegenwoordig geen snoertjes meer bij komen kijken, wordt de term nog steeds gebruikt in de kontekst van de diverse MIDI-gestuurde synthesizers. De wijze waarop de FM-synteze algoritmes worden samengesteld en gekombineerd wordt ook steeds met de term 'patch' aangeduid.
De blokjes waarover we nu elk in drievoud beschikken kunnen symbolisch worden voorgesteld als:
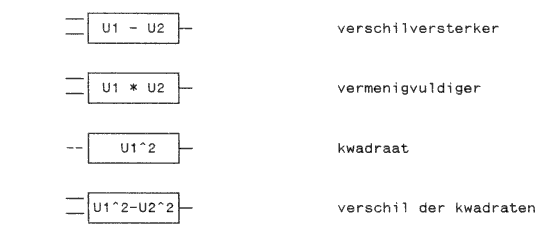
De signalen U1 en U2 in de blokjes kunnen worden gesubstitueerd door hetzij de X,,Z, en C signalen van het ingangsblok, hetzij door uitgangssignalen van andere voorgeschakelde blokjes.
We hebben systematisch gebruik gemaakt van de patchmogelijkheden van de volgende twee symmetrische vormen:- gemeenschappelijke modulator-patch: (4 ingangen) GMP
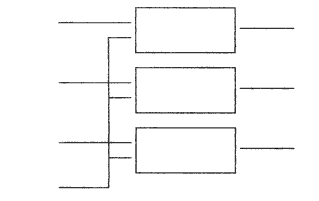
- mutual-modulator patch: (3 ingangen) : MMP
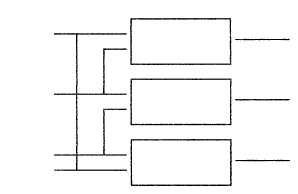
De door ons geteste patches kunnen samengevat worden als volgt:
- MMP- mogelijkheden
- met [U1*U2] blokken:
- met [U1^2-U2^2] blokken:
- gevolgd door [U1^2] blokken:
- gevolgd door [U1-U2] blokken:
- GMP- mogelijkheden
- met U1*U2 blokken:
- met [U1^2-U2^2] blokken:
- gevolgd door [U1^2] blokken:
- gevolgd door [U1-U2] blokken:
- GMP met X*C, Y*C, Z*C gevolgd door MMP met ofwel de multiplier-funktie ofwel het verschil der kwadraten.
Wanneer de ruis diende geminimalizeerd te worden, volstond het vaak rechtstreeks MMP met de multiplier funktie te gebruiken.
2.3.4 Evaluatie
Voor de beoordeling van de mogelijkheden opgeleverd door de verschillende patch-konfiguraties zijn we meer uitgegaan van het bekomen klankrezultaat dan wel van de geimpliceerde rekenkundige bewerkingen. Dit is minder 'on-rationeel' dan het op het eerste zicht lijkt. Immers wanneer we in de instrumentale opstelling bewegen zijn we ideaal geplaatst om de relevantie van de motorische input in het klinkende geluid te evalueren. Het gaat er uiteindelijk toch om een zo groot mogelijke korrelatie te vinden tussen expressieve bewegingsmotoriek en eigenschappen van een klankrezultaat. Zo levert de MMP patch met [U1*U2] blokken het beste rezultaat wanneer het erop aankomt zo duidelijk mogelijk de bewegingssnelheid in sonore eigenschappen te vertalen. De GMP patches met [U1*U2] blokken zijn dan weer veel geschikter wanneer het erop aankomt de ruimtelijkheid van de bewegingen in de klanken te vertalen. Wat betreft vertaling van wat we zelf als motorische inspanning ervaren, zijn de blokken met kwadraatfunkties dan weer beter geschikt, alleen zijn de door deze blokken voortgebrachte geluidssignalen veel 'onmuzikaler' dan die van de overige blokken. Dit heeft veel te maken met de sterk asymetrische signalen die door deze blokken worden voortgebracht.
Overigens dient gezegd, dat onze empirische rezultaten door rekenkundige analyze kunnen bevestigd worden.
2.3.4.1.: Simulatie-programma
Om hier echter vele toch vrij moeilijk leesbare rekenkundige afleidingen te vermijden, kunnen we dit ook grafisch duidelijk maken. Daartoe schreven we het betrekkelijk uitgebreide komputerprogramma 'HOLOSIMI.EXE' voor MS-DOS machines (de ruim bekommentarieerde listing van het programma werd toegevoegd in de appendix en een gekompileerde versie ervan staat ook op de diskbijlage), waarmee zowat alle met de analoge komputer instelbare rekenkundige funkties en bewegingsmodellen kunnen gesimuleerd worden en getoond in een grafiek waarop de in- en uitgangssignalen in de tijd worden uitgezet.
| Wie het programma wil laten lopen dient wel over een snelle MS-DOS machine te beschikken uitgerust met een 80486DX processor (of een 80386DX-80387 kombinatie) omdat het gebruik maakt van enorm veel vlottende-komma operaties, waardoor het op een 'ormale' machine zenuwslopend traag gaat. Bovendien moet de komputer uitgerust zijn met een VGA scherm dat in screen-mode 12 kan worden aangestuurd. |
Het programma laat toe zeer dicht de werkelijke ingangssignalen zoals die voorkomen in het werkende instrument en zoals ze verschijnen op een oscilloskoopscherm te benaderen, maar eveneens laat het toe om -terwille van het inzicht in parametrische korrelaties- vereenvoudigde signalen in te voeren. Anders dan het geval was bij onze inleidende wiskundige beschouwingen gegeven sub. 2.1.2, werkt het hier geimplementeerde model wel degelijk 3-dimensioneel. Daarvoor werd uitgegaan van een realistische tijd-ruimtelijke topografie van een bewegend volume door een tetraederruimte.
Het model waarbinnen het programma 'Holosimi' werkt heeft echter toch nog steeds volgende beperkingen:
- - alle gesimuleerde bewegingen van een volume worden beschouwd over een rechtlijnig en dus één-dimensioneel trajekt P1->P2.
Stel X,,Z, zijn de hoekpunten van een gelijkzijdige driehoek gevormd door de drie ontvangers. Stel C bevindt zich op het aan deze driehoek toe te voegen hoekpunt om een regelmatig viervlak te vormen. De rechte vanuit C naar het middelpunt/zwaartepunt van driehoek X,,Z snijdt het vlak van de driehoek dus loodrecht. De koordinaten van deze ruimte laten dus toe deze laatste in vier kwadranten te verdelen. Dit koordinatenstelsel kan men zich het best voorstellen als een kraaiepoot.
Het trajekt van P1 naar P2 is beperkt tot de grenzen van de omschreven bol bepaald door deze tetraeder.
Gezien deze veralgemening, geldt de betrekking die we aantoonden sub. 2.2., formule (4) voor de onderlinge relatie tussen de Dopplerfrekwenties zoals ontvangen door X, en Z:- fz = fx + fy
De rechte waarop de beweging wordt geacht plaats te vinden wordt eenduidig bepaald door het opgeven van de drie afstanden van X, Y, Z, tot het beginpunt van de beweging en tot het eindpunt ervan. - - Het model (maar hierin komt het eigenlijk vrij goed overeen met de werkelijkheid) laat niet toe te bepalen of een beweging aan de C kant van de tetraeder dan wel aan de tegenovergestelde kant plaatsgrijpt. De reden daarvoor is dat de door de analoge komputer voortgebrachte frekwenties absolute waarden zijn. Wiskundig gezegd: het teken gaat in de konversie verloren. In ons model gaat echter nog meer informatie verloren omdat de meeste hoeken herleid werden tot het eerste kwadrant. Hadden we dit niet gedaan, dan hadden we niet kunnen ontsnappen aan het vrij omslachtige werken met imaginaire getallen in het programma.
Vierkantswortels uit sinussen of cosinussen van hoeken kunnen negatieve waarden hebben onder de wortel, waarvoor zonder introduktie van imaginaire getallen geen oplossing kan gevonden worden. BASIC heeft wat dit betreft helaas ook geen speciale voorzieningen.
Deze beperking verklaart het soms optreden van eigenaardige knikken in de verkregen kurves, o.i. te wijten aan de fazedraaiing die gevolg is van een reduktie tot het eerste kwadrant, bij bepaalde bewegingen, meer bepaald wanneer daarbij de lijnen van de tetraeder-koördinaten worden overschreden. - - Het bewegend volume wordt beschouwd als een bol (symmetrisch en weerkaatsend in alle richtingen dus) met oppervlakte S. Deze bol wordt vanuit elk der hoekpunten gezien als een cirkel-oppervlak, analoog aan de wijze waarop wij de maan waarnemen. Net zoals in de astronomie, wordt hier terdege rekening gehouden met de relatieve verschillen in waargenomen bewegingssnelheid in funktie van de diameter van deze cirkel. Precies dit element laat ons toe via de analoge komputer en de verder beschreven digitale verwerking van de gegevens informatie te verwerven over de grootte van het bewegend oppervlak.
- - De simulatie van het gereflekteerd Doppler-signaal bestaat uit een gewogen optelsom van maximaal het in de variabele Rd (16 tot 256) bepaalde aantal sinusvormige kurves, volgens volgende finitistisch benaderende formule:
- n->Rd
Ux = Σ { [ Sin(k * (Fx + ((Bfx * n) / Rd)) * t] * Ix }
n=0
- Rd = densiteit van het beschouwde signaal
Bfx = bandbreedte van het beschouwde signaal
t = tijd
k = rad. konversiekonstante
Fx = laagste frekwentie van het verschilsignaal op moment t.
Ix= amplitude van het signaal p moment t in funktie van oppervlak en kwadraat van de afstand tegenover X.
- n->Rd
- - De fazedraaiingen die optreden in het systeem werden buiten beschouwing gelaten. Zolang de grootte van het beschouwde bewegend oppervlak immers veel groter is dan de golflengte van de draaggolf ( voor een 40kHz ultrasoonsignaal in lucht is dat dus 340m/s / 40000Hz= 8.5mm), kunnen we stellen dat de fazedraaiingen elkaar in het eindsignaal grotendeels uitmiddelen. Ook dient men zich te realizeren dat de fazedraaiing meerdere volledige periodes kan belopen.
- - De eerste stap in de signaalverwerking moet verlopen volgens de hiervoor geschetste MMP-patch. Binnen deze patch kunnen volgende funkties ingesteld worden:
- MMP-vermenigvuldiger
- MMP-verschil der kwadraten
- MMP-verschilversterker
- MMP-opteller (mixer)
- MMP-logaritme van een quotient
- Limiteren (begrenzen)
- Schmitt-Trigger (blokpulsvormer)
- Integreren met een instelbare tijdkonstante
- Differentieren over een instelbaar interval
- Nul-doorgangsdetektie
- MMP-vermenigvuldiging
- MMP-verschil der kwadraten
- MMP-verschilversterker
- MMP-opteller (Mixer)
- - Het gehele programma maakt systematisch gebruik van finitistische wiskunde: alle integralen worden herleid tot eindige permanente sommen en alle differentialen tot eindige verschillen. Afgezien van onze filozofische overtuiging terzake, kan daartegen geen bezwaar worden ingebracht, aangezien ook de elektronische meerkanaalsoscilloskopen evenals de in het volgend hoofdstuk behandelde digitale verwerking, uitgaan van samples en dus van eindige diskontinue funkties.
2.3.4.1.1.: Legende bij de symbolen in de verder gebruikte grafieken:
S = maat voor de oppervlakte van het bewegend volume.
Deze parameter is veranderlijk in het simulatieprogramma. Dit komt overeen met de mogelijkheid ons instrument te bespelen via kontraktie- en expansiebewegingen, zoals bvb. het openen van een vuist naar een gestrekte hand, wat gepaard gaat met een oppervlakte-toename.
Hoe kleiner dit oppervlak, hoe smalbandiger het gereflekteerde Dopplersignaal zal zijn. Hoe groter het bewegend oppervlak, hoe groter de ruisbandbreedte. In het limietgeval (wanneer S=0) beschouwen we een bewegend punt. Dit zou dan aanleiding geven tot een zuiver sinusvormig Dopplerverschilsignaal. Maar, aangezien een punt hier niet bestaan kan -en indien het al zou bestaan, zeker geen reflekterend oppervlak kan hebben waarmee een verschilsignaal zou kunnen gereflekteerd worden, is dit een louter platonisch model.
Men moet zich S dan ook voorstellen als de maximale afmeting van een bol die rechtlijnig door de instrument-ruimte beweegt. De bol kan klein beginnen en vergroten in de loop van de beweging, of andersom, tot een 'punt' verschrompelen tijdens zijn beweging in het ruimtevlak. Ook het verloop van de bewegingssnelheid kan via een reeks funkties worden ingesteld.
α = de hoek tussen het lijnstuk van P1 naar P2 en de lijn ZP1. Deze hoek wordt opgegeven in radialen waarbij dus 180° = π Rad.
Vmax. = De hoogste snelheid die de bol in de loop van zijn beweging bereikt. Deze parameter wordt opgegeven door de gebruiker van het programma.
Elke grafiek die rezultaat is van het simulatieprogramma bestaat uit zes verschillende kurves, in volgorde:- - het gedemoduleerde Doppler-verschilsignaal van de ontvanger opgesteld in hoekpunt X. Dit signaal bevat rechtstreeks de vektoriele snelheidsinformatie.
- - het rezultaat van de ingestelde bewerking op de signalen van X en Y. De funktie staat als memo aangegeven boven of onder de kurve.
- - het gedemoduleerde Doppler-verschilsignaal van de ontvanger opgesteld in hoekpunt Y.
- - het rezultaat van de ingestelde bewerking op de signalen van Y en Z.
- - het gedemoduleerde Doppler-verschilsignaal van de ontvanger opgesteld in hoekpunt Z
- - het rezultaat van de ingestelde bewerking op de signalen van Z en X.
1e letter:
-
A = Vermenigvuldiger
B = Verschil der kwadraten
C = Som
D = Verschil
E = Log van het quotient
F = RC Low-pass filter
G = RC High-pass filter
H = Kwadraat
- R = Uitgaand van een bewegende bol
S = Uitgaand van een puntmassa en sinussignalen
F = Uitgaand van een model van toononzekerheid bij
de beschouwing van een bewegend lichaam
K = Uitgaand van een bewegende kegel waarvan de punt zich in het centrum van de kraaiepoot bevindt. ( voor latere implementatie)
- Bewegingsmodel m.b.t. snelheidsverloop in de tijd:
A = Eenparig rechtlijnige beweging
B = snelheidsverloop als halve sinuskurve
C = versnellend volgens 1/4-sinuskurve
F = konstante versnelling
G = konstante vertraging
I = snelheidsverloop volgens een beta-kurve met twee parameters
- Bewegingsmodel m.b.t. oppervlakteverloop in de tijd:
A = bol met konstante straal
B = straal verlopend volgens 1/2 sinuskurve (π)
C = straal verlopend volgens 1/2 cosinuskurve (π)
D = straal verlopend volgens 1/4 sinuskurve (π/2)
E = straal 1/4t lineair omhoog 1/2t konstant 1/4t lineair afnemend tot 0 F = straal lineair toenemend
G = straal lineair krimpend
H = straal volgens |1-Cos| over π
I = straal verlopend volgens een beta-funktie met twee parameters
- geen = geen verdere analoge verwerking
^ = gekwadrateerd rezultaat
_ = begrensd rezultaat
B = blok-puls signaal Schmitt-trigger
* = vermenigvuldigd
+ = gesommeerd
- = verschil
f = geintegreerd
| = gedifferentieerd
0 = nuldoorgangsdetektor
d = verschiltoonfiltering
s = somtoonfiltering
We zullen pogen in een beknopte kommentaar bij de hiernavolgende kurves een duiding te geven m.b.t. de aard van de beweging en de korrelatie aan sonore eigenschappen van het klinkend rezultaat of van het informationeel rezultaat. Om de lezer geblader naar de hierboven gegeven legende te besparen hebben we de kommentaar bij elke kurve als een parameter-lijst toegevoegd.
2.3.4.1.1.1.: Muzikale reprezentatie van de simulaties
Voor een aantal van de bewegingen hebben we ook voorzien in een voorstelling van een muzikaal analogon van door de analoge komputer verkregen bewegingsinformatie. Deze voorstellingswijze is -we kunnen het niet genoeg benadrukken- geenszins bedoeld als 'muziek' ondanks het feit dat we er klassiek notenschrift voor gebruiken. We hebben het alleen gedaan omdat het aan musici en muzikologen vaak een beter inzicht in de betekenis van de kurves geeft, dan een grafische voorstelling. De in noten weergegeven simulaties werden net zoals de grafische, gegenereerd door mijn 'Holosimi' programma. Ze kunnen ook worden afgespeeld via dezelfde komputer en wat -overigens ook in deze studie beschreven- door ons ontwikkelde randapparatuur. Ook bezitters van een Roland MPU-401 interface worden door het programma ondersteund.
In deze muzikale simulaties worden vooral veranderingen van het frekwentieverloop van de kurves erg goed duidelijk. In een grafisch weergegeven kurve kan men ze slechts waarnemen als kleine veranderingen tegenover de wiskundige vorm van normale sinussen. Vergeten we immers niet dat de frekwentie in werkelijkheid in elk tijdsinterval verschillend is wanneer een rechtlijnige beweging door de ruimte wordt beschouwd. Alleen bij eenparige cirkelvormige bewegingen tegenover een waarnemingspunt is een gelijkblijvende frekwentie van het Doppler-signaal teoretisch denkbaar.
De genoteerde toonhoogtes komen strikt overeen met de intervallen en intervalverhoudingen onder de frekwenties zoals ze door het onzichtbare instrument in deze ruwe vorm worden voortgebracht. Omwille van de noteerbaarheid werd ermee volstaan hen te 'projekteren' op een gelijkzwevend gestemd 'piano'-klavier. De ritmische notatie is even akkuraat als de weergave in de grafische kurves. De notatie in 20 maten laat echter een grotere rezolutie toe dan het geval is in de grafische kurves, waarbij we de baanintervallen in sekties van 10% van de afgelegde weg van het beschouwde trajekt onderverdeelden. In beide voorstellingsvormen echter, worden 640 punten berekend.
Voor de muzikale reprezentatie zijn dat dan 640 32-ste noten, wat in een 4/4maat (overeenkomstig een indeling per 5%) dus precies 20 maten oplevert. Het maatcijfer is overigens volkomen arbitrair.
Nadeel van de muzikale reprezentatie in de vorm van een notenbeeld is dat het grootste deel van de in de kurves besloten dynamische informatie verloren gaat. Waar in onze verdere analyzes dit facet het meest in het oog springt, geven we dan ook geen muzikale reprezentatie. De reprezentatie in klinkende vorm anderzijds, volgt heel getrouw -binnen de 7-bit beperking opgelegd door het MIDI-systeem- de dynamiek van de getekende kurves.
2.3.4.1.2.: Grafische & muzikale simulaties
Omwille van de grafische duidelijkheid hebben we de bewegingssnelheid in het simulatieprogramma veel lager genomen dan in de praktijk zelfs maar mogelijk is (nml. 0.5 tot 5mm/s!).
Dit is uitsluitend een kwestie van schaal en heeft geen enkele invloed op de analyze zelf.
Om het verloop van de tekst niet tezeer in het gedrang te brengen, behandelen we hier slechts enkele bewegingsmodellen, en van elk model geven we slechts enkele reprezentatieve kurves. Ter vervollediging werden de rezultaten van heel wat andere bewegingen en simulaties, aan de appendix toegevoegd. Een volledigheid op het punt van de analyze van de motorische expressie hebben we hier niet nagestreefd. Dit zal het onderwerp vormen van een later onderzoek, waarbij we hopen een koppeling te kunnen maken tussen motorische expressie, retoriek en wat Manfred Clynes 'Sentics' doopte. Wat hier van belang is, is dat we hopen te kunnen aantonen dat de motorische eigenschappen van diverse bewegingen wel degelijk kunnen teruggevonden worden in de door onze apparatuur verwerkte signalen. Hoe deze signalen dan terug in relevante muzikale gebeurtenissen kunnen worden omgezet, vormt dan het onderwerp van hoofdstuk 3.
We beperken ons hier dan ook tot volgende sterk vereenvoudigde bewegingstypes of modellen:-
TYPE 1:
- vlottende bewegingen: regelmatige bewegingen met konstante snelheid en betrokken lichaamsoppervlak over een relatief lange rechte baan.
TYPE 2:
- expanderende bewegingen met toenemend lichaams-oppervlak. (Groeiend.)- SUB-TYPE 1:
- SUB-TYPE 2:
- SUB-TYPE 3:
TYPE 3:
- kontraherende bewegingen met afnemend lichaams-oppervlak. (Krimpend).- SUB-TYPE 1:
- SUB-TYPE 2:
- SUB-TYPE 3:
TYPE 4:
- afgeronde en gesloten bewegingen. Deze types hebben een duidelijk begin en einde. Het zijn op zich gesloten vormen of 'bewegings-zinnen'.- SUB-TYPE 1:
- SUB-TYPE 2:
De sub-types met volgnummer hoger dan 2, lieten we eveneens weg uit de hiernavolgende beschouwingen. Zij kunnen eenvoudig worden ingezien uit kombinaties van de gegeven hoofdmodellen, en bovendien zijn ze aan te treffen in de appendices sub 5.2.3.
2.3.4.1.2.1.: TYPE 1: Vlottende bewegingen
2.3.4.1.2.1.1.: ARAA-kurves
Bewegingsmodellen met eenparig rechtlijnige beweging en konstante bewegingsoppervlakte.Kurves met volgende gemeenschappelijke parameters:
Eigenschappen van de bewegingsruimte:
- Zijde van de ruimte-tetraeder = 3 m
Straal van de omschreven bol = 1.632993 m
- Straal van het objekt = 20 cm
Reflekterend oppervlak = 1256 cm^2
- Lengte van de beschreven baan = 116 cm
Hoogte van het eerste punt t.o.v. XYZ = 61 cm
Hoogte van het tweede punt t.o.v. XYZ = 37 cm
De beweging verloopt dalend naar XYZ toe
De beweging verloopt weg van de zender
Hoogste bewegingssnelheid = 2 mm/s
De beweging was eenparig rechtlijnig
- De oppervlakte van het objekt was konstant
Aard van de komputersimulatie:
- De beweging verloopt op een rechte bepaald door de twee opgegeven punten met koordinaten P(X,Y,Z,C):
(de vierde koordinaat wordt berekend)- P1( 1 , 2 , 3 , 2.23)
P2( 2 , 1 , 3 , 2.45)
- P1( 1 , 2 , 3 , 2.23)
- De beweging gaat doorheen het XYZ-vlak.
- Het bewegend objekt wordt beschouwd als een bol. Het erdoor gereflekteerd signaal is een som van 16 sinussen.
- Konstanten: Geluidssnelheid = 340 m/s / Ultrasoonfrekwentie = 40 kHz
Om het bewegingsverloop grafisch duidelijk te maken geven we voor elke verschillende beweging een projektie van het verloop op het tetraedervlak XYZ. Opgemerkt moet worden dat in de praktische opstelling van het onzichtbaar instrument, dit vlak -enigszins kontra-intuitief misschien- niet het grondvlak of de bodem is! Het fyzische bodemvlak wordt in onze opstelling gevormd door de driehoek XYC, waarbij dus de zender op de bodem voor de speler wordt geplaatst.
| In de opstelling voor de muziekteaterkompositie 'Holosound' bevindt de zender zich achter de speler, en de ontvangers X, links en rechts voor hem. In het later ontwikkelde ' Book of Moves' (cfr. hoofdstuk 3) veranderden we dit naar een frontale opstelling van de zender, dit in eerste plaats om interferentie met het publiek te vermijden. De opstelling van de derde ontvanger, het punt Z in onze modellen, is voor beide gevallen de top van de denkbeeldige tetraeder. Dit levert het beste rezultaat omdat ook de hoogtebewegingen op deze wijze optimaal gekapteerd kunnen worden. Deze beschouwing moge voor de lezer meteen ook verklaren waarom we in onze modellen geen bezwaar hebben gemaakt tegen de wiskundige mogelijkheid (en werkelijkheid) dat een punt in de tetraederruimte bepaald door de 3 afstanden tot de punten X,,Z slechts twee-duidig bepaald kan worden. Er zijn steeds twee mogelijke oplossingen: één in de reële tetraeder en één in zijn virtuele antipode tegenover het vlak XYZ. |
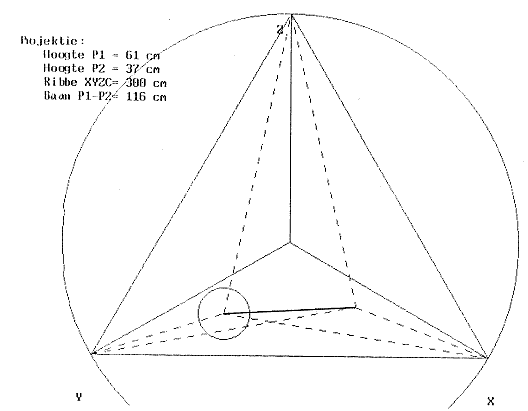
KURVES ARAA/001
Analoge komputer patches:
| Multiplier: | (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t) | |
| (Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t) | ||
| (Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t) |
Schaalfaktoren:
- Koëfficiënten kurves X,,Z = .25
Koëfficiënten kurves X*Y, Y*Z, Z*X = .08
Ter illustratie drukten we van de X,,Z kurves eveneens het 'muzikaal' equivalent af. In het verloop van de toonhoogtes komen af en toe eigenaardige oktaafsprongen voor. (bvb. maat 3 stem X). Deze hebben klaarblijkelijk te maken met een bug in het muzieknotatieprogramma zelf. (Het Amerikaanse 'oteprocessor' van Stephan Dydo). De door onze software gegenereerde muzieknotatiekode vertoont de afwijking in elk geval niet.
Op te merken valt dat het melodisch verloop hier een beter idee geeft van de veranderlijke frekwentie van de signalen dan wat kan blijken uit een louter vizuele analyze van de overeenkomstige kurves. De amplitude-informatie echter, gaat in het omzettingsproces helemaal verloren.
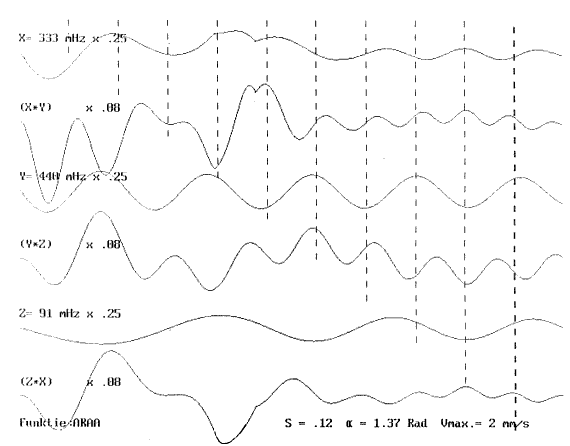



KURVES ARAA/002
Hoogste bewegingssnelheid = 4 mm/s
Analoge komputer patches:
| Multiplier: | (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t) (Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t) (Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t) |
Schaalfaktoren:
- Koëfficient kurve X,,Z = .25
Koëfficient kurve X*Y,*Z,X*Z = .2
De hier beschreven beweging en de signalen erdoor veroorzaakt verschilt van de vorige alleen inzake bewegingssnelheid. Het beschouwde trajekt schiet een heel eind voorbij aan het opgegeven eindpunt van het trajekt. Duidelijk zichtbaar is dat de amplitudes van alle signalen, bij het verlaten van de beschouwde bewegingsruimte, naar nul gaan.
In deze kurves, door de hogere waarde voor de bewegingssnelheid worden ook de som- en verschiltonen in het vermenigvuldigd signaal bijzonder duidelijk: de verschiltoon kan heel goed gezien worden in de omhullende van Y*Z. De somtonen zijn in alle produktkurves goed te zien. De mogelijkheden van de beschikbare apparatuur -in eerste plaats dan de niet-beschikbaarheid van een goede vlakbedplotter- lieten ons niet toe de kurves met hogere waarden voor de snelheden te tekenen vanwege het gering oplossend vermogen van de matrix-printers die we gebruikten.
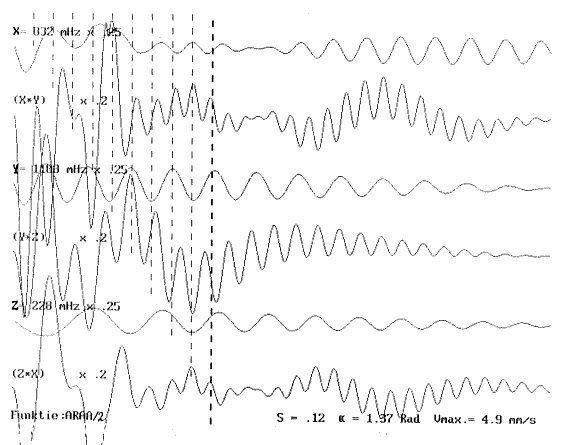
KURVES ARAAB.001
Vooral om de werking van de geïmplementeerde Schmitt-trigger in ons 'Holosimi'-programma duidelijk te maken, voegen we deze kurves toe. Alle parameters zijn identisch aan die van ARAA.001, behalve de instelling van de tweede orde analoge komputer.
Samengevat:
- Bewegingssnelheid = 2 mm/s
Analoge komputer patches:- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- Multiplier:
Schaalfaktoren:
De schaalfaktoren werden hier automatisch ingesteld via een daartoe geschreven subprogramma. (cfr. appendix). Uit deze waarden kan wel een goed idee bekomen worden over de piek-amplitudes die bereikt worden in de loop van een beweging, aangezien de schaal-routine de maxima en minima van de amplitudes opzoekt om daaruit de koëfficiënten te berekenen. De in de kurves afgedrukte koëfficiënten voor de tweede-orde kurves hebben geen voor de kurves relevante betekenis, aangezien het hier om louter binaire waarden gaat.
- Koëfficiënt kurve X=.3329929
Koëfficiënt kurve Y=.4036232
Koëfficiënt kurve Z=.5400805
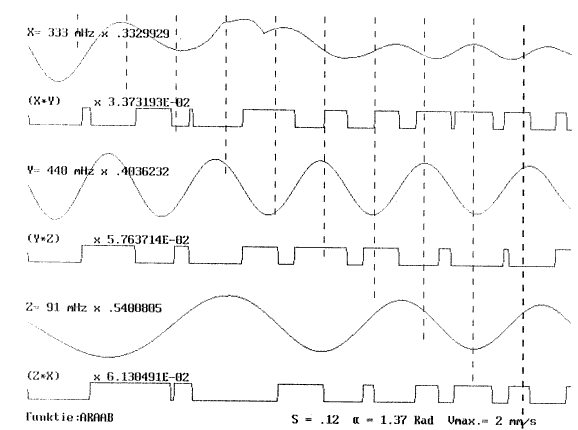
De werking van de nul-doorgangsdetektor zal duidelijk worden uit het beschouwen van de desbetreffende kurve:
KURVES ARAA0.001
De aperiodiciteit van de pieken in de produktkurves is hier erg opvallend. Door de dichtheid van deze pieken te meten (aantal pieken per tijdseenheid) kan de oorspronkelijke bewegingssnelheid worden afgeleid.
Analoge komputer patches: Multiplier:
- Zero-cross van (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
Zero-cross van (Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
Zero-cross van (Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
Schaalfaktoren:
- Koëfficiënt kurve X, Y, Z = .25
Koëfficiënt kurve X*0Y, Y*0Z, Z*0X = 3
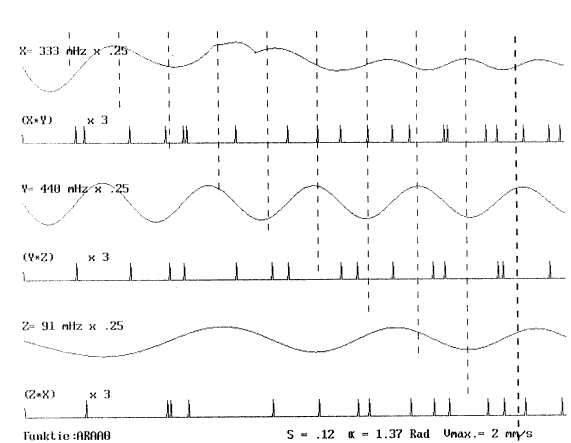
KURVES BRAA.001
Voor deze kurves werd de analoge komputer ingesteld voor de berekening van het verschil der kwadraten van X,,Z. Deze kurve werd afgedrukt op een schaal identisch aan die van ARAA.001, om vergelijkingen gemakkelijker te maken. Deze kurve verloopt heel wat geprofileerder dan die van ARAA. Het verloop van deze kurve vertoont ook niet de uitgesproken piek bij het begin van de beweging die de ARAA kurve kenmerkt. Deze bewerking kan vooral dan gebruikt worden wanneer het vermogen van een beweging in een signaal beschikbaar moet worden gesteld.
Analoge komputer patches: Verschil der kwadraten:
- [(Ix.Sin(2.π.Fx.t)^2] - [(Iy.Sin(2.π.Fy.t)^2]
[(Iy.Sin(2.π.Fy.t)^2] - [(Iz.Sin(2.π.Fz.t)^2]
[(Iz.Sin(2.π.Fz.t)^2] - [(Ix.Sin(2.π.Fx.t)^2]
Schaalfaktoren:
- Koëfficiënt kurve X, Y, Z = .25
Koëfficiënt kurve XrY , YrZ, ZrX= .08
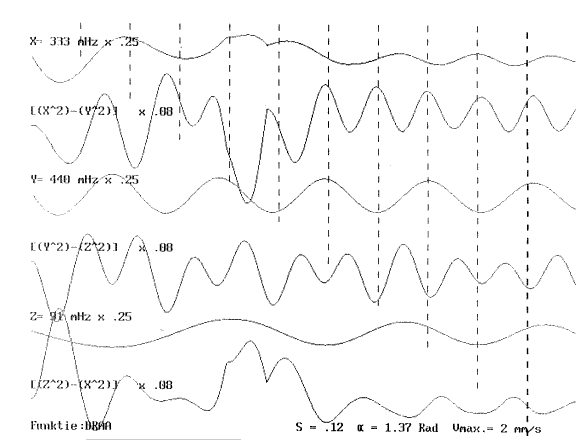
We zien dat de rezulterendesignalen bij het begin van de beweging vaak een zeer grotere dynamiek vertonen. In de praktijk gaan de signalen in gevallen die dit benaderen (dus een zeer abrupte overgang van stilstand naar beweging) buiten de limieten van de mogelijke uitgangssignalen, elektro-technisch uitgedrukt: er treedt clipping op. Dit was op wiskundige grond eenvoudig te verklaren uit het feit dat we hier een beweging in een tijd gelijk aan nul laten beginnen en eindigen. Volgens de Fourier-analyze zou zo' diskontinue overgang (een loodrechte signaalflank) inderdaad een 'oneindig' spektrum moeten hebben. De versnelling zou immers oneindig groot moeten zijn...
Om dit probleem in ons simulatieprogramma te ondervangen hebben we de signalen netjes in faze laten beginnen bij het begin van elk kurve. Hierdoor wordt dit effekt al zeer goed afgezwakt en komt de simulatie ook een heel stuk dichter bij de werkelijkheid te staan.
Zo'n kurve brengt ons het bijzonder nuttige inzicht dat 'diskontinue' of in motorische termen gesteld 'abrupte' bewegingen en bewegingsovergangen aanleiding kunnen geven tot sterke verhogingen van de momentane amplitudes der uitgangssignalen van de vermenigvuldigers. Dit is een muzikaal heel bruikbaar rezultaat aangezien het toelaat motorische impulsen in een elektrisch equivalent signaal om te zetten.
Willen we dit aspekt uit het signaal naar voor halen, dan zullen we de analoge komputer instellen op kwadraat-funkties. De asymetrische pieken die dan ontstaan kunnen weggewerkt worden via integratie.
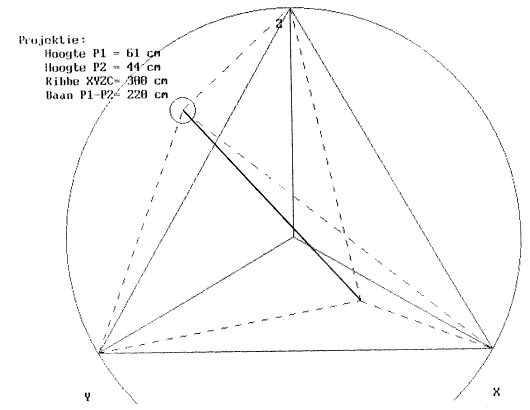
Parameters voor deze vlottende beweging:
Eigenschappen van het bewegend objekt:
- Straal van het objekt = 10 cm
Reflekterend oppervlak = 314 cm^2
Eigenschappen van de beweging:
- Lengte van de beschreven baan = 220 cm
Hoogste bewegingssnelheid = 4 mm/s
De beweging was eenparig rechtlijnig
- De oppervlakte van het objekt was konstant
Aard van de komputersimulatie:
- De beweging verloopt op een rechte bepaald door de twee opgegeven punten met koordinaten P(X,Y,Z,C):
P1( 1 , 2 , 3 , 2.2) : P2( 3 , 2 , 1 , 2.2) - Het bewegend objekt wordt beschouwd als een bol
Het gereflekteerd signaal is een som van 16 sinussen
- (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- De kurves tonen de kwadraten van de vorige bewerkingen.
- Koëfficiënt kurve X,,Z = 1
Koëfficiënt kurve XhY, YhZ, ZhX = .2
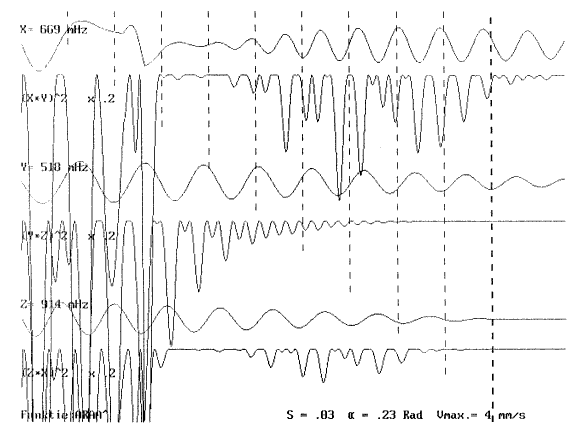
Tot slot van deze vlottende bewegingssimulaties, en om de som- en verschiltonen duidelijk te maken geven we op de volgende bladzijden, twee simulaties waarbij de kurves respektievelijk alleen de uitgefilterde verschil en somtonen laten zien. Uit deze frekwenties kan de bewegingssnelheid makkelijk worden afgeleid. In de analoge realizatie van 'Holosound' zijn deze tonen ook duidelijk hoorbaar.
De hier niet opgenomen parameters waren zoals in de vorige modellen.
Eigenschappen van het lichaam:
- Straal van het objekt = 15 cm
Reflekterend oppervlak = 706 cm^2
- Lengte van de beschreven baan = 228 cm
Hoogte van het eerste punt t.o.v. XYZ = 54 cm
Hoogte van het tweede punt t.o.v. XYZ = 37 cm
De beweging verloopt dalend naar XYZ toe en weg van de zender.
Konstante bewegingssnelheid = 4 mm/s
- P1( 3 , 2 , 1 , 2.14 ) : P2( 1 , 2 , 3 , 2.45 )
- (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
Schaalfaktoren:
- Koëfficiënt kurve X,,Z = 1
Koëfficiënt kurve X-Y,-Z,Z-X = 2
Schaalfaktoren:
- Koëfficiënten voor alle kurves = 1
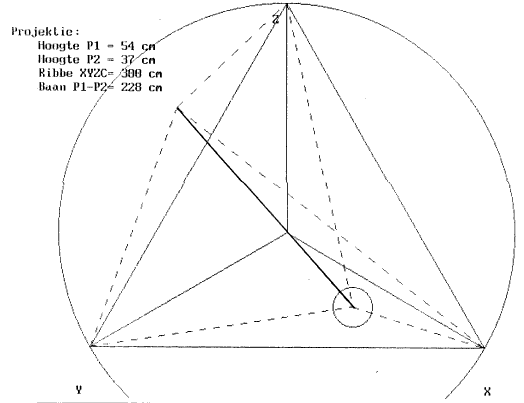
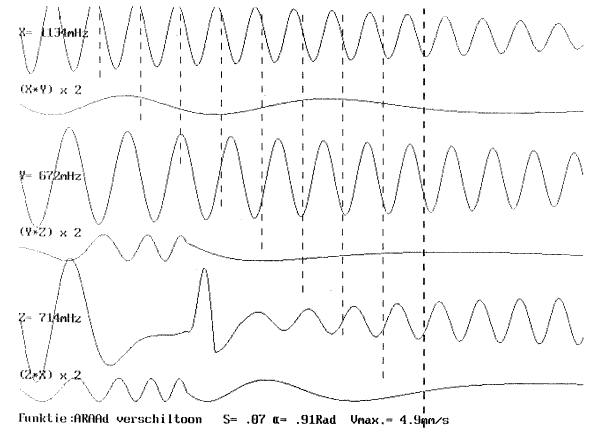
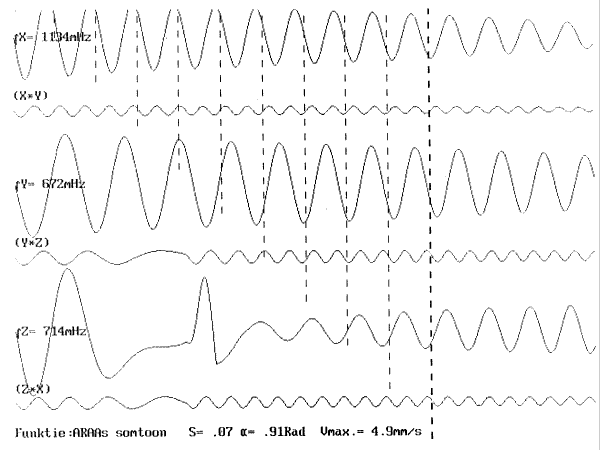
2.3.4.1.2.2.: TYPE 2:
Expanderende bewegingen
Simulaties van bewegingen waarbij de oppervlakte van het bewegend volume lineair toeneemt. Dit type bewegingen heeft een grote expressieve signifikantie: het zijn bewegingen die als expansief, extravert, explosief enzomeer kunnen worden aangeduid. We geven hierbij twee sub-types geillustreerd aan de hand van signaalkurves en equivalenten daarvan in klassiek notenschrift.232122.1.: SUB-TYPE 1:
de teatrale botsing.
We hebben deze beweging zo genoemd omdat ze iets leugenachtigs insluit, immers een toenemende lichaamsmassa waarbij de bewegingssnelheid omgekeerd evolueert is een expressieve paradox.Gemeenschappelijke parameters voor deze groep:
Software: Holosound-simulator V9.3
Eigenschappen van de bewegingsruimte:
- Zijde van de ruimte-tetraeder = 3 m
Straal van de omschreven bol = 1.632993 m
Eigenschappen van het bewegend objekt:
- Straal van het objekt = 15 cm
Reflekterend oppervlak = 706 cm^2
Eigenschappen van de beweging:
- Lengte van de beschreven baan = 75 cm
Hoogte van het eerste punt t.o.v. XYZ = 49 cm
Hoogte van het tweede punt t.o.v. XYZ = 49 cm
Verloop van de grootte van het bewegend objekt in de tijd:
De oppervlakte van het lichaam verliep volgens een beta-funktie met de parameters bpiA= 2 en bpiB= 0.
Aard van de komputersimulaties:
- De beweging verloopt op een rechte bepaald door de twee opgegeven punten met koordinaten P(X,Y,Z,C). De vierde koordinaat wordt berekend door het programma.
- P1( 1 , 2.2 , 1.9 , 2)
P2( 2 , 2.4 , .8 , 2)
- P1( 1 , 2.2 , 1.9 , 2)
- Het bewegend objekt wordt beschouwd als een bol. Het erdoor gereflekteerd signaal is gesimuleerd als een som van 16 sinussen. De bandbreedte is een funktie van de grootte van de beschouwde bol.
- Konstanten:
- Geluidssnelheid = 340 m/s
Ultrasoonfrekwentie = 40 kHz
- Geluidssnelheid = 340 m/s
KURVES ARII:
Specifieke parameters:
Piek-bewegingssnelheid = 1.7mm/s
Analoge komputer patches:
- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- Voor alle getekende kurves = 1
Van dit bewegingsmodel maakten we ook een voorstelling in notenschrift.
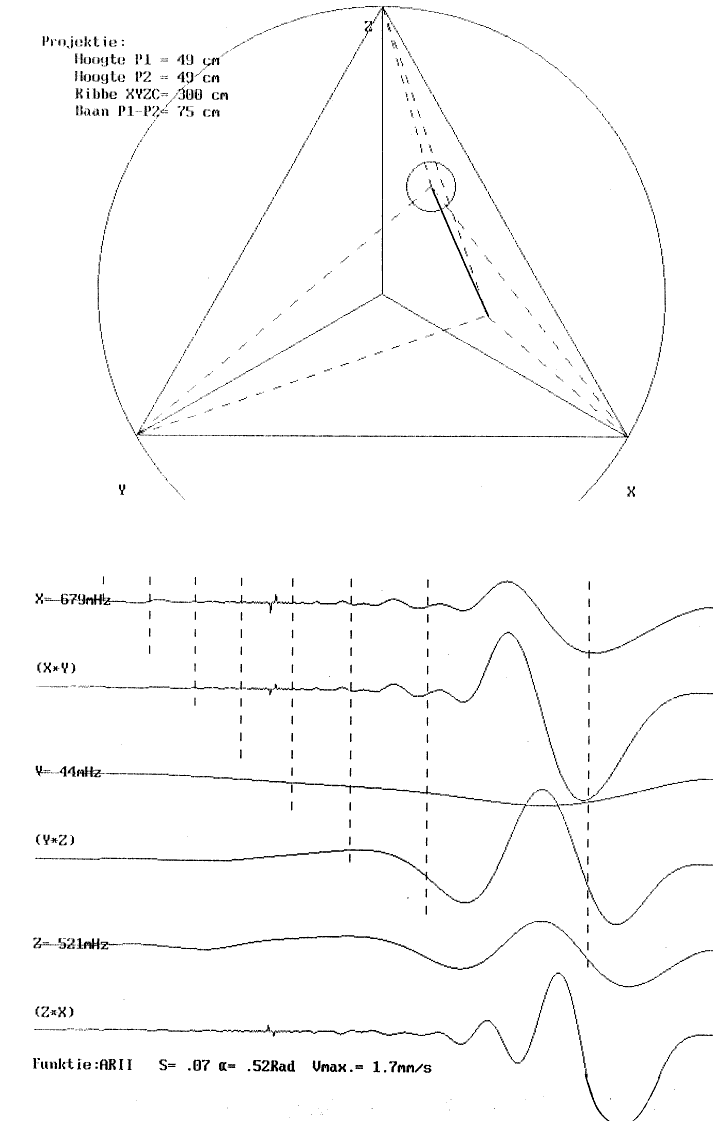

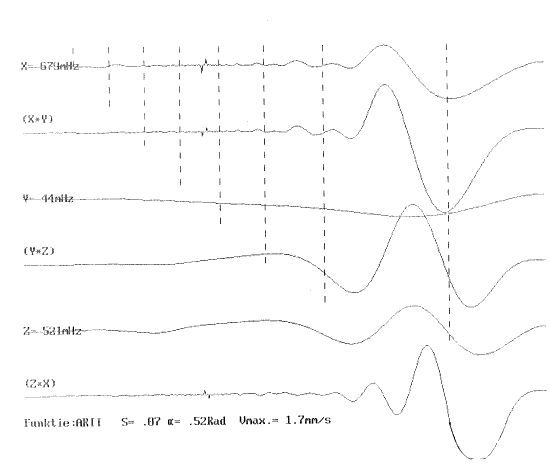



KURVES ARII0
Hoogste bewegingssnelheid = 2 mm/s
Analoge komputer patches:
- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- De weergegeven kurves werden bewerkt door een nul-doorgangs detektor, hierdoor wordt de snelheids-informatie uit het signaal opnieuw ge-extraheerd.
- Voor alle kurves = 1
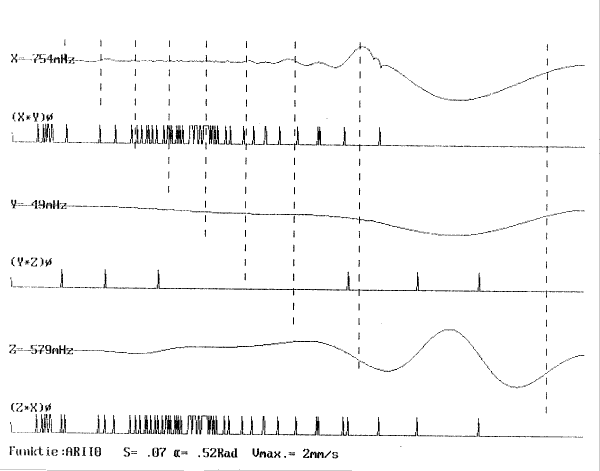
KURVES ARIIF
Hoogste bewegingssnelheid = 2 mm/s
Analoge komputer patches:
- Multiplier:
1/RC ⌠(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)⌡
1/RC ⌠(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)⌡
1/RC ⌠(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)⌡
- De kurves voor XfY, YfZ, ZfX werden hier geintegreerd. De integratie RC-tijdkonstante was ingesteld op 30. De kurve toont het AC signaal na filtering door een Low-pass filter.
Schaalfaktoren:
- Voor alle kurves= 1
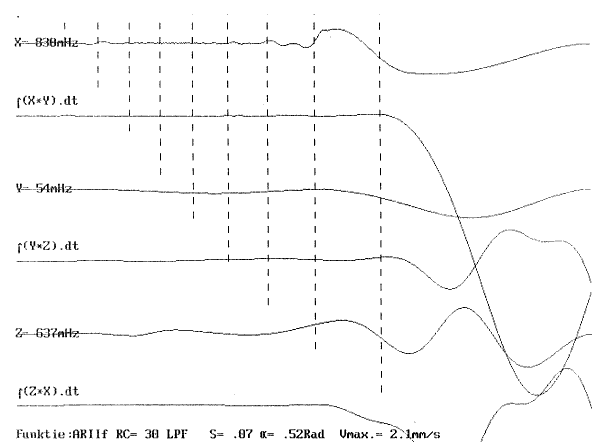
232122.2.: SUB-TYPE 2:
de explosieve beweging of botsing
Gemeenschappelijke parameters voor deze groep kurves en simulaties:Software versie:
- Holosound simulator V9.3
Eigenschappen van de bewegingsruimte:
- Zijde van de ruimte-tetraeder = 3 m
Straal van de omschreven bol = 1.632993 m
Eigenschappen van het bewegend objekt:
- Straal van het objekt = 15 cm
Reflekterend oppervlak = 706 cm^2
Eigenschappen van de beweging:
- Lengte van de beschreven baan = 53 cm
Hoogte van het eerste punt t.o.v. XYZ = 77 cm
Hoogte van het tweede punt t.o.v. XYZ = 127 cm
De beweging verloopt stijgend, naar de zender toe
De bewegingssnelheid nam steeds toe van nul naar dit maximum volgens een kwart-sinuskurve.
Verloop van de grootte van het bewegend objekt in de tijd: De oppervlakte van het objekt nam lineair toe als een funktie van de tijd tot het opgegeven maximum
Aard van de komputersimulatie:
- De beweging verloopt op een rechte bepaald door de twee opgegeven punten met koordinaten P(X,Y,Z,C):
- P1( 1.8 , 1.9 , 2 , 1.67)
P2( 2 , 2.1 , 2.4 , 1.21)
- P1( 1.8 , 1.9 , 2 , 1.67)
- Het bewegend objekt wordt beschouwd als een bol. Het erdoor gereflekteerd signaal is gesimuleerd als een som van 16 sinussen.
- Konstanten:
- Geluidssnelheid = 340 m/s
Ultrasoonfrekwentie = 40 kHz
- Geluidssnelheid = 340 m/s
KURVES ARCF:
Specifieke parameters:
- Bewegingssnelheid= 1.7mm/s
- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- Voor alle kurves = 1
Het explosief karakter van de signalen volgt duidelijk uit het verloop van de spanningen zoals getekend in de vermenigvuldigingskurves.
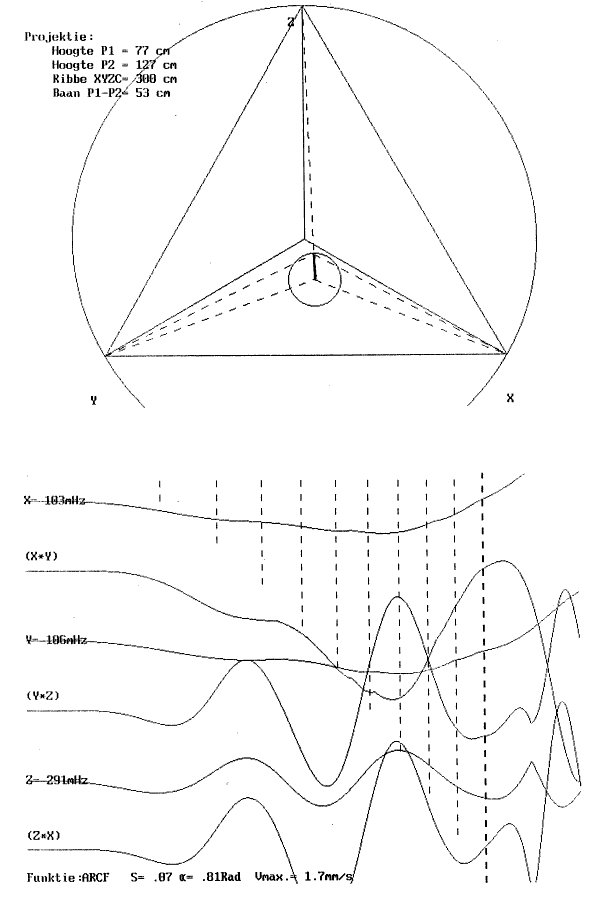
Door de trage gekozen snelheid is het frekwentieverloop niet erg goed te zien, daarvoor kan men beter de ARCF0-kurve nakijken en deze vergelijking met de overeenkomstige kurve weergeven bij type 2, sub 1.
Specifieke parameters voor deze kurves:
Analoge komputer patches:
Multiplier:
- (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- De kurves werden bewerkt door een nul-doorgangs detektor
Schaalfaktoren:
- Voor alle kurves = 1
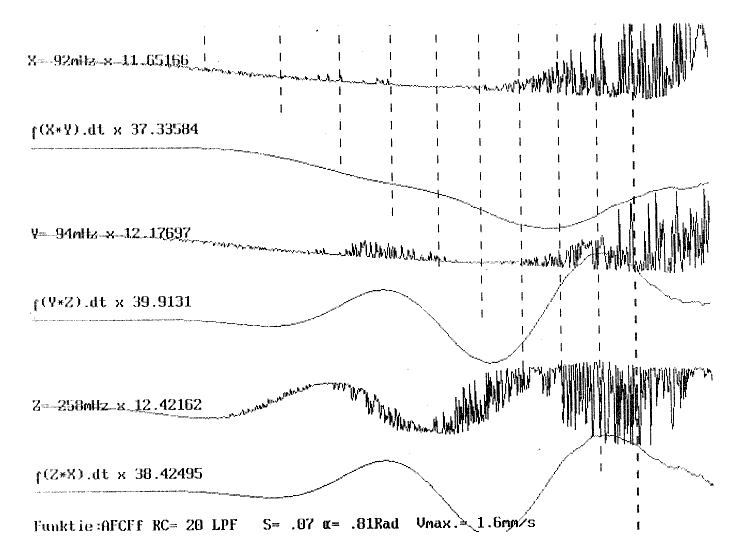
Ook wanneer we in plaats van een additieve ruissimulatie een onzekerheidsruis-simulatie toepassen en het rezultaat van de bewerking integreren, blijft de signifikantie van de kurves behouden, zoals blijkt uit volgende kurves AFCFf.
Specifieke parameters:
-Het door het als bolvormig beschouwd objekt weerkaatst signaal werd beschouwd als een frekwentie met een onzekerheidsfaktor in funktie van de hier lineair toenemende grootte van de beschouwde bol.
Analoge komputer patches:
- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- De kurves voor XfY, YfZ, ZfX werden geintegreerd. De integratie RC-tijdkonstante was ingesteld op: 2. De kurve toont het AC signaal na filtering door een Low-pass filter.
Schaalfaktoren:
- Koëfficiënt kurve X = 11.65166
Koëfficiënt kurve Y = 12.17697
Koëfficiënt kurve Z = 12.42162
Koëfficiënt kurve XhY = 37.33584
Koëfficiënt kurve YhZ = 39.9131
Koëfficiënt kurve ZhX = 38.42495

Willen we uit een bewegingsverloop vooral het amplitude-dynamisch karakter naar voor halen, dan kan de kwadraat-funktie ook hier heel veel diensten bewijzen, zoals blijkt uit volgende HRCF-kurve.
Specifieke parameters:
Hoogste bewegingssnelheid = 1.6 mm/s
Analoge komputer patches:
- Kwadraatkurves:
{[(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)]^2}
{[(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)]^2}
{[(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)]^2}
Schaalfaktoren:
- Voor alle kurves = 1
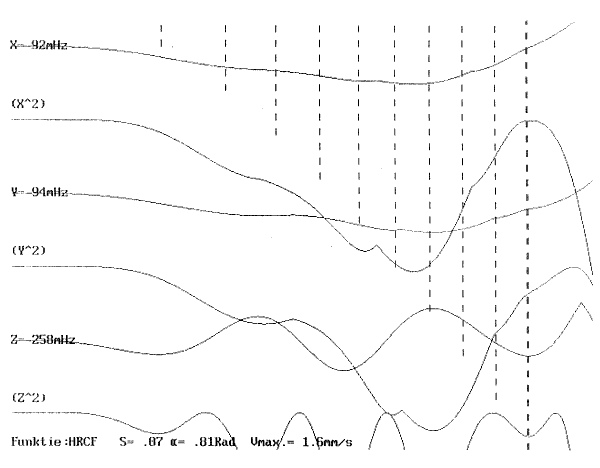
Van het X,Y,Z signaalverloop geven we ook hier een 'muzikale' reprezentatie in klassiek notenschrift. Omdat de dynamiek hier buiten beschouwing blijft, en alleen de opgewekte toonhoogtes omgezet worden naar korresponderende noten, ziet dit verloop er erg verschillend uit van de grafische kurves. Het zal duidelijk zijn dat het melodisch verloop een goede afspiegeling geeft van de snelheidskomponenten van de gesimuleerde beweging.



2.3.4.1.2.3 TYPE 3 : Kontraherende bewegingen
Simulaties van bewegingen waarbij de oppervlakte van het bewegend volume afneemt in funktie van de tijd. Dit zijn bewegingsvormen die we als kontrakties zouden kunnen beschrijven en die ook een grote motorisch-expressieve relevantie kunnen hebben. We onderscheiden met betrekking tot het verloop van de bewegingssnelheid volgende gevallen:234123.1.: SUB-TYPE 1: Imploderende bewegingen
Gemeenschappelijke parameters voor de kurves van deze simulatie:Software versie: Holosound simulator V9.3
Eigenschappen van de bewegingsruimte: idem.
Eigenschappen van het bewegend objekt:
- Straal van het objekt = 20 cm
Reflekterend oppervlak = 1256 cm^2
- Lengte van de beschreven baan = 166 cm
Hoogte van het eerste punt t.o.v. XYZ = 4 cm
Hoogte van het tweede punt t.o.v. XYZ = 29 cm
De beweging verloopt stijgend naar C en naar de zender toe.
Hoogste bewegingssnelheid = 5 mm/s. De bewegingssnelheid nam lineair af van dit maximum tot nul. (Konstante vertraging).
Aard van de komputersimulatie:
- De beweging verloopt op een rechte bepaald door de twee opgegeven punten met koordinaten P(X,Y,Z,C).
- P1( 2 , 1 , 2.6 , 2.6 ) : P2( 2.6 , 2 , 1 , 2.3 )
- Het bewegend objekt wordt beschouwd als een bol. Het gereflekteerd signaal is gesimuleerd als een som van 16 sinussen.
- Konstanten: idem.
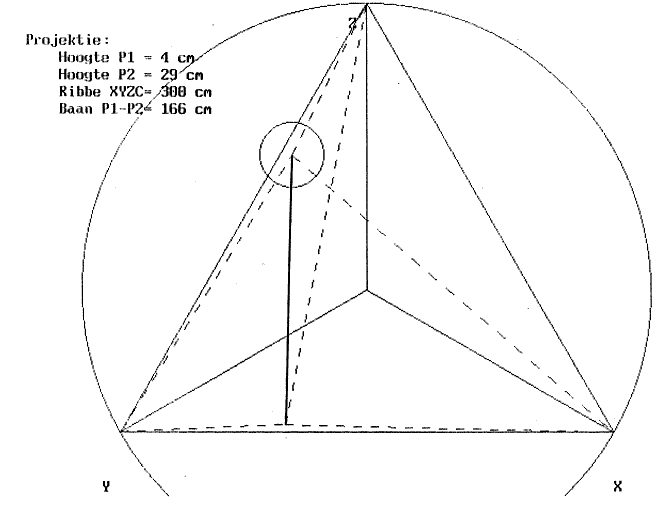
KURVES ARGG
Specifieke parameters:
Maximale bewegingsssnelheid: 4.9mm/s
Analoge komputer patches:
- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
Schaalfaktoren:
- Koëfficiënten kurves X, , Z = .7
Koëfficiënten kurves XΦY, YΦZ, ZΦX = .5
De kurves zowel als de motorische beweging die gesimuleerd werd zijn erg 'logisch' omdat het vertragen en het inkrimpen parallel verlopen.
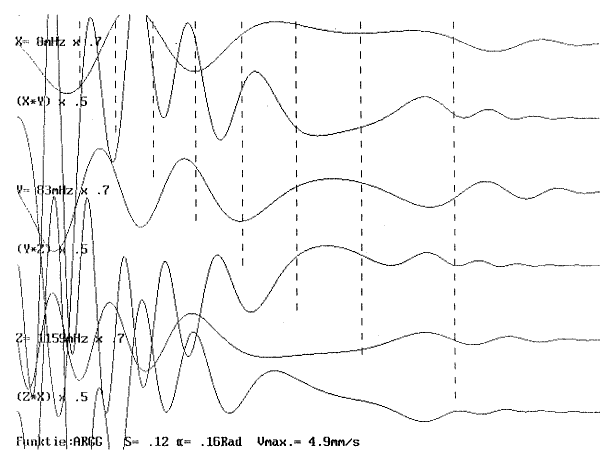
Willen we van hieruit het amplitudeverloop naar voren halen, dan is een integratie van het kwadraat van de X, Y , Z kurves bijzonder geschikt, zoals blijkt uit de volgende kurve HRGGf.
Specifieke parameters:
Hoogste bewegingssnelheid = 5.6 mm/s
- De bewegingssnelheid nam daarbij lineair af van dit maximum tot nul, dus een konstante vertraging.
Analoge komputer patches:
- Kwadraatkurves:
{[(Ix.Sin(2.c.Fx.t).(Iy.Sin(2.c.Fy.t)]^2}
{[(Iy.Sin(2.c.Fy.t).(Iz.Sin(2.c.Fz.t)]^2}
{[(Iz.Sin(2.c.Fz.t).(Ix.Sin(2.c.Fx.t)]^2}
- De kurves voor XfY, YfZ, ZfX werden geintegreerd. De integratie RC-tijdkonstante was ingesteld op 10. Dit laat nog vrij veel schommelingen zien in de rezulterende kurves. Stellen we RC in op bvb. 40, dan verdwijnen de schommelingen geheel. De kurves tonen het verloop van de gelijkgerichte signaalspanning op een kondensator. Het model is dat van een afgevlakte gelijkspanning, onbelast.
- Koëfficiënt kurve X =.50 : Koëfficiënt kurve Y= .428
Koëfficiënt kurve Z= .511: Koëfficiënt kurve fx^2 = 6.5E-02
Koëfficiënt kurve fy^2 =4.58E-02 :Koëfficiënt kurve fz^2 =6.53E-02- Door tweemaal een vermenigvuldiger in te schakelen verkrijgen we als het ware een karikatuur in signaalvorm van de imploderende beweging. De kurve is in de appendix opgenomen (ARGG*).
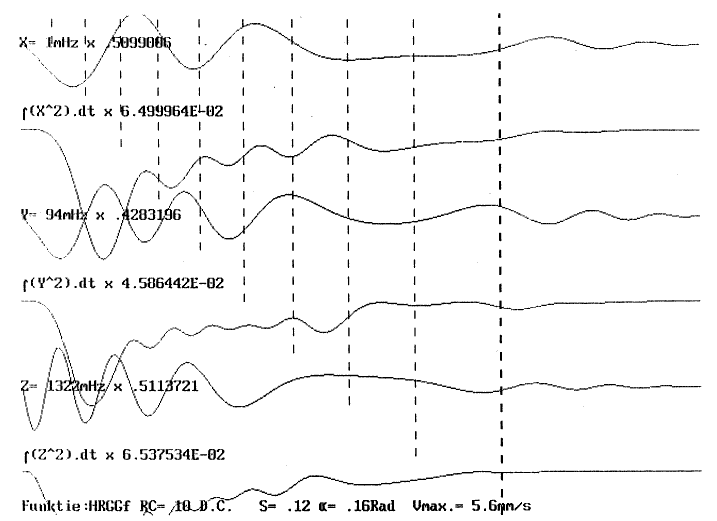
234123.2.: SUB-TYPE 2: Vluchtende bewegingen
Model van evaderende of vluchtende bewegingen, waarbij het lichaamsvolume afneemt en de bewegingssnelheid toeneemt.Gemeenschappelijke parameters voor deze bewegingssimulaties:
Eigenschappen van de bewegingsruimte: idem.
Eigenschappen van het bewegend objekt:idem.
Eigenschappen van de beweging:
- Lengte van de beschreven baan = 166 cm
Hoogte van het eerste punt t.o.v. XYZ = 4 cm
Hoogte van het tweede punt t.o.v. XYZ = 29 cm
De beweging verloopt stijgend naar C en naar de zender toe
Hoogste bewegingssnelheid =5 mm/s. De bewegingssnelheid nam lineair toe van nul tot dit maximum, wat neerkomt op een konstante versnelling.
- De beweging verloopt op een rechte bepaald door de twee punten: P1( 2 , 1 , 2.6 , 2.59) en P2( 2.6 , 2 , 1 , 2.30)
- Het bewegend objekt wordt beschouwd als een bol. Het gereflekteerd signaal is een som van 16 sinussen
- Konstanten: idem.
KURVES ARFG:
Specifieke parameters:
Analoge komputer patches: Multiplier:
- (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- Koëfficiënten kurves X, Y, Z=1: Koëfficiënten kurves X*Y,*Z,Z*X=0.5
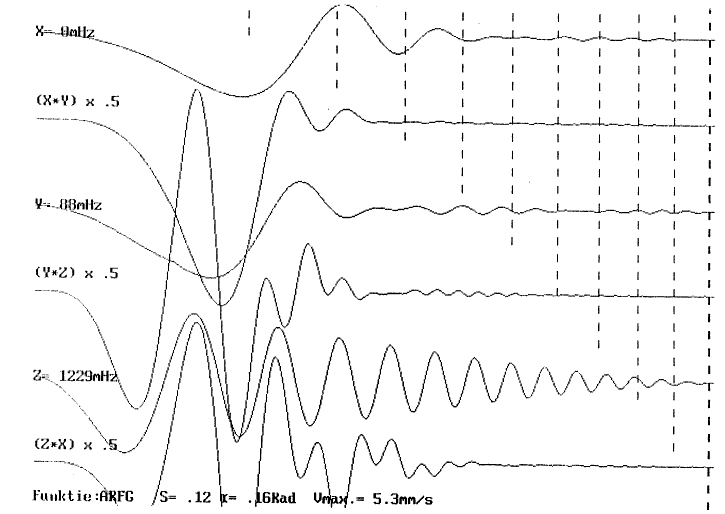
Integratie van deze kurves levert ons een beeld van de bewegingsamplitude op.
Specifieke parameters:
Analoge komputer patches: Multiplier:
- (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- De kurves voor X*Y, Y*Z, Z*X werden geintegreerd. De integratie RC-tijdkonstante was ingesteld op 40. De kurve toont het verloop van de spanning op een kondensator. Het model is dat van een afgevlakte gelijkspanning, onbelast.
- Koëfficiënten kurves X, Y, Z = 1
Koëfficiënten kurves fX*Y,FY*Z,fZ*X = 0.3
Omdat het volume naar nul gaat bij het einde krijgen we hier geen abrupt signaal te zien. Deze beweging komt goed overeen met wat een dirigent zou doen om na een decrescendo een orkest gelijk te doen zwijgen.
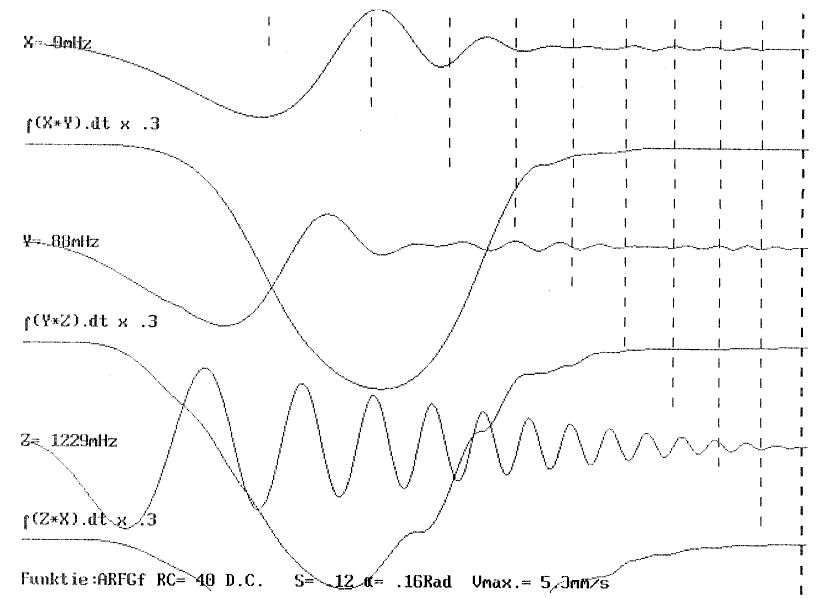
Het versnellend verloop is uit het signaal van de vermenigvuldigers goed af te leiden, wanneer we op de analoge komputer de nul-doorgangsdetektor inschakelen.
Specifieke parameters:
Analoge komputer patches:
- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- De kurves werden bewerkt door een nul-doorgangs detektor
Schaalfaktoren:
- Voor alle kurves : 1
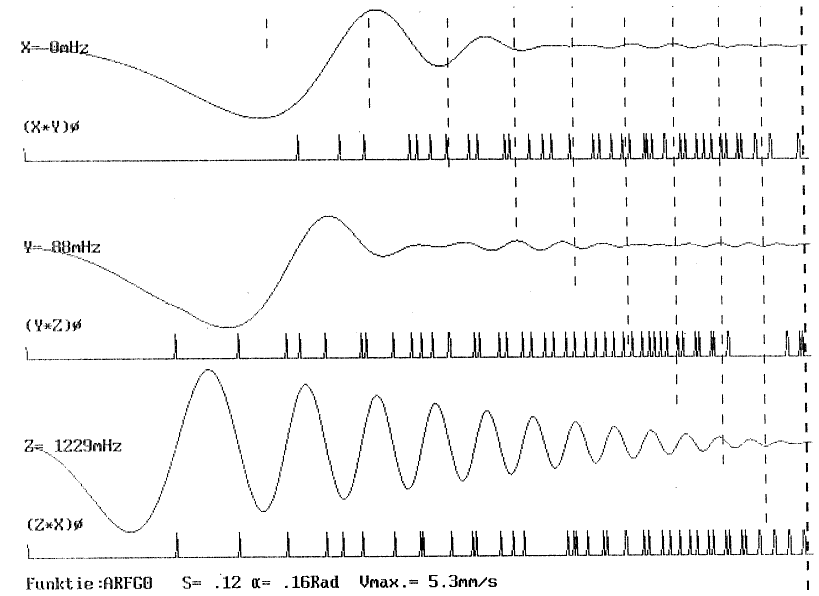
2.3.4.1.2.4.: TYPE 4: Gesloten bewegingsvormen
Hier gaat het om bewegingen met een korte tijdsduur en een duidelijke begrenzing van begin en einde. Anders gesteld: elke beweging vertrekt vanaf stilstand en eindigt ook met een stilstand.234124.1.: TYPE 4 - SUB-TYPE 1 : Metrische impuls
Gemeenschappelijke parameters:Eigenschappen van de bewegingsruimte: idem.
Eigenschappen van het bewegend objekt:
- Straal van het objekt = 15 cm
Reflekterend oppervlak = 706 cm^2
- Lengte van de beschreven baan = 140 cm
Hoogte van het eerste punt t.o.v. XYZ = 45 cm
Hoogte van het tweede punt t.o.v. XYZ = 18 cm- De beweging verloopt dalend naar XYZ toe, en dus weg van de zender.
- De bewegingssnelheid verliep volgens een beta-funktie bepaald door de parameters bpfA= 3 en bpfB= 3 (zie toegevoegde beta-kurve).
- De oppervlakte van het objekt was konstant.
Aard van de komputersimulatie:
- De beweging verloopt op een rechte bepaald door de twee opgegeven punten met koordinaten P(X,Y,Z,C):
- P1( 1.8 , 1 , 2.4 , 2.1 ) : P2( 2.5 , 2 , 1 , 2.4 )
- Het bewegend objekt wordt beschouwd als een bol. Het gereflekteerd signaal is een som van 16 sinussen
- Konstanten: idem.

KURVES ARIA:
Specifieke parameters:
Analoge komputer patches:
- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
Schaalfaktoren:
- Koëfficiënten kurves X, Y, Z = 1
Koëfficiënten kurves XΘY, YΘZ, ZΘX = .25
Opmerkelijk in deze kurves -meer bepaald in die waarin het rezultaat van de vermenigvuldigers wordt weergegeven, is de dubbele puls die ontstaat en het gevolg is van de omkering van het verloop van de bewegingssnelheid. Dit rezultaat is muzikaal gezien heel erg bruikbaar omdat het snelheidsomkeringen profileert. Hierdoor is het mogelijk de ritmiek van een beweging uit de signalen te distileren.
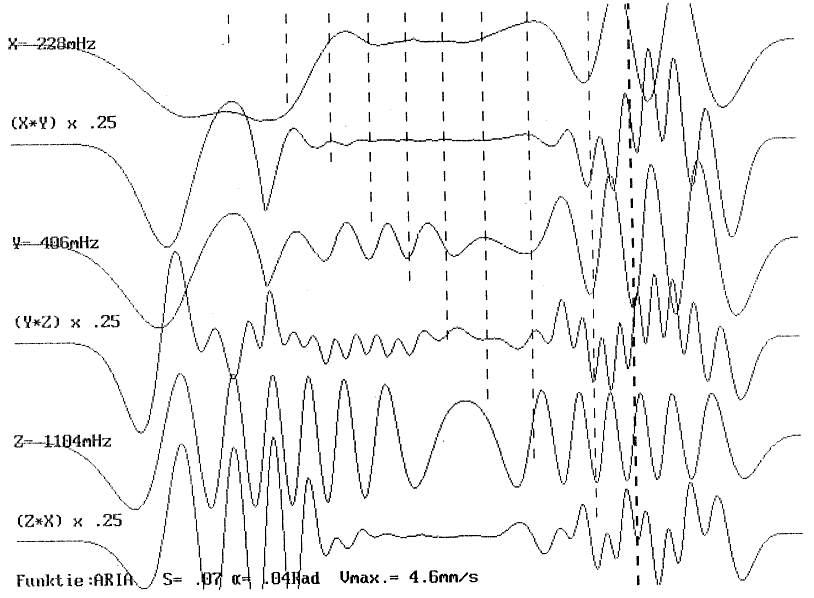
Wanneer we het rezultaat van de vermenigvuldiging integreren, zoals gedaan in volgende kurves, wordt dit nog heel wat duidelijker.
Specifieke parameters:
Analoge komputer patches:
- Multiplier:
(Ix.Sin(2.c.Fx.t).(Iy.Sin(2.c.Fy.t)
(Iy.Sin(2.c.Fy.t).(Iz.Sin(2.c.Fz.t)
(Iz.Sin(2.c.Fz.t).(Ix.Sin(2.c.Fx.t)
- De kurves voor XfY, YfZ, ZfX werden geintegreerd. De integratie RC-tijdkonstante was ingesteld op 30. De kurves tonen het verloop van de gelijkgerichte spanning op een kondensator. Het elektronisch model is dus dat van een afgevlakte gelijkspanning, onbelast.
Schaalfaktoren:
- Voor alle kurves = 1
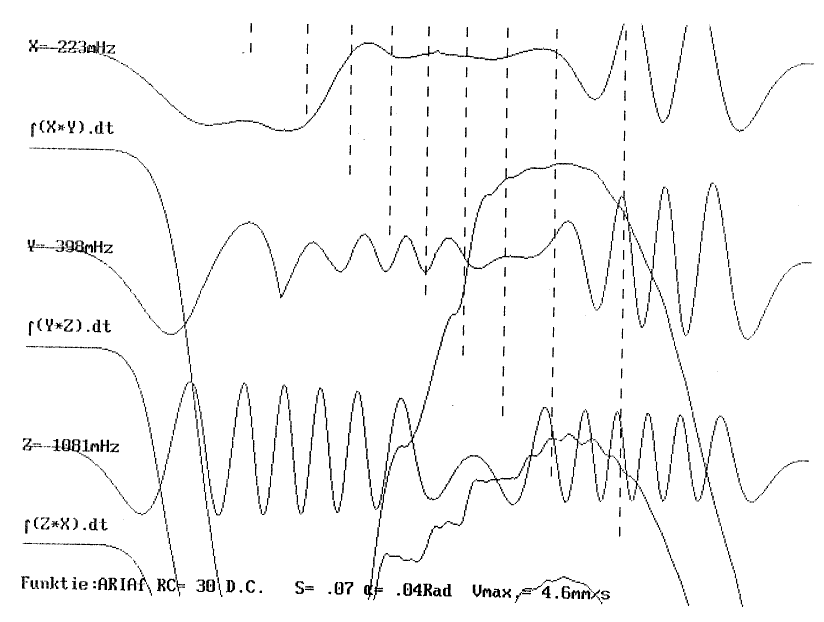
234124.2: TYPE 4 - SUB-TYPE 2 : Perkussieve impuls
Gemeenschappelijke parameters voor deze bewegingssimulaties:Eigenschappen van de bewegingsruimte: idem.
Eigenschappen van het bewegend objekt:
- Straal van het objekt = 15 cm
Reflekterend oppervlak = 706 cm^2
- Lengte van de beschreven baan = 51 cm
Hoogte van het eerste punt t.o.v. XYZ = 90 cm
Hoogte van het tweede punt t.o.v. XYZ = 44 cm
De beweging verloopt dalend naar XYZ en weg van de zender.
Hoogste bewegingssnelheid = 2 mm/s- De bewegingssnelheid verliep volgens een beta-funktie bepaald door de parameters bpfA= 4 en bpfB= 4.
- De oppervlakte van het lichaam verliep volgens een beta-funktie met de parameters bpiA= 4 en bpiB= 4.
Aard van de komputersimulatie:De beweging verloopt op een rechte bepaald door de twee punten:P1(1.8 , 2.3 , 1.6 , 1.6), P2(2 , 1.9 , 1.5 , 2 )
- Het bewegend objekt wordt beschouwd als een bol. Het gereflekteerd signaal is gesimuleerd als een som van 16 sinussen.
- Konstanten:idem.
De geprojekteerde beweging op het vlak XYZ geven we op de volgende bladzijde, evenals een grafische weergave van de beta-kurves met parameters 4,4. Voor zowel oppervlakte-verloop als voor snelheidverloop werd eenzelfde kurve gebruikt.
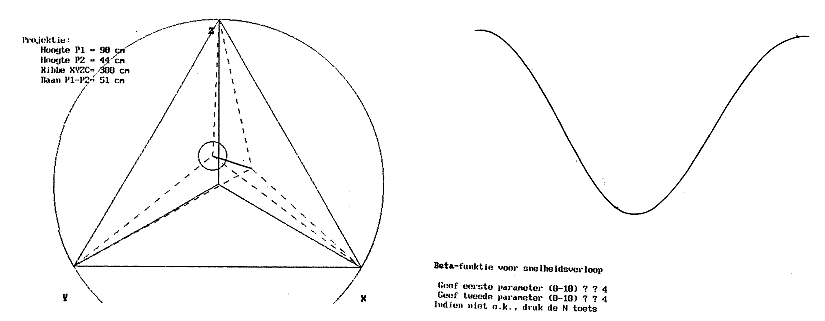
KURVES ARII
Specifieke parameters:
Analoge komputer patches:
- Multiplier:
(Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
- Koëfficiënt kurve X = .7073771
Koëfficiënt kurve Y = .7141141
Koëfficiënt kurve Z = .7271255
Koëfficiënt kurve X*Y = .1342774
Koëfficiënt kurve Y*Z = .1385935
Koëfficiënt kurve Z*X = .1290176
In tegenstelling tot de kurves weergegeven in onze beschrijving van het vorige model, de metrische puls, is hier geen duidelijke dubbele puls meer waar te nemen. Het perkussieve karakter van de beweging blijft behouden in de signalen.
In de fyzische werkelijkheid zal de muzikus dit type beweging bijna steeds uitvoeren als een over-en-weer gaande beweging. (Cfr. onze beschrijving van de trommelslag in hoofdstuk 1). De vektoriele richting van de beweging zou hier dus eigenlijk omgekeerd moeten worden op het moment dat de beweging haar hoogste snelheid bereikt. In de huidige versie van onze software kan dit echter niet worden geimplementeerd doordat we in onze berekeningen de funkties met kwadraten implementeerden met uitsluitend reële getallen. Door dit vermijden van imaginaire getallen, zijn negatieve snelheden, negatieve richtingen e.d. niet op eenvoudige wijze te behandelen. We hopen dit in een latere versie van de software toch te kunnen voorzien. Overigens zal dergelijke uitbreiding geen principiele wijzigingen veroorzaken aan de besluiten die we menen te mogen trekken uit de hier naar voor gebrachte rezultaten.
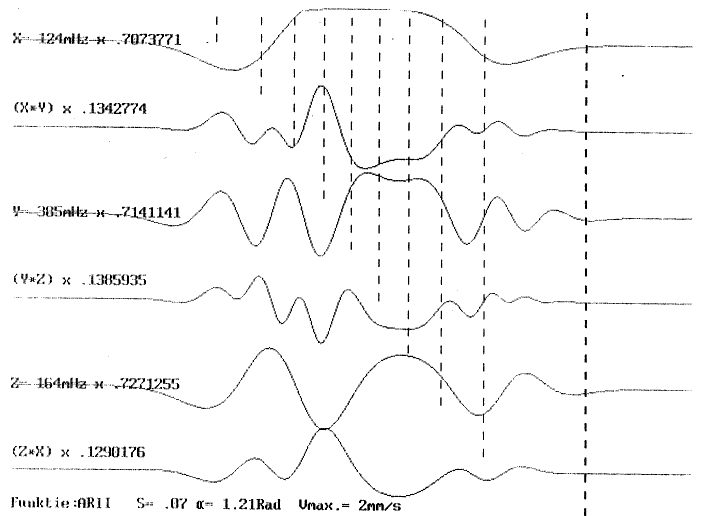
De omhullende van de slag -in de input van het programma bepaald door een beta-kurve met parameterkoppel 4,4- kan gerekonstitueerd worden, zoals tevoren, via integratie van het vermenigvuldigd signaal, zoals moge blijken uit volgende kurve:
Kurves ARIIf-DC:
Specifieke parameters:
Hoogste bewegingssnelheid = 1.9 mm/s
Analoge komputer patches: Multiplier:
- (Ix.Sin(2.π.Fx.t).(Iy.Sin(2.π.Fy.t)
(Iy.Sin(2.π.Fy.t).(Iz.Sin(2.π.Fz.t)
(Iz.Sin(2.π.Fz.t).(Ix.Sin(2.π.Fx.t)
Schaalfaktoren:
- Koëfficiënt kurve X = .5 : Koëfficiënt kurve Y, Z = 1
Koëfficiënt kurve X*Y = .5, Y*Z = .3, Z*X = .1
Omdat de 'muzikale' reprezentatie hier perfekt het frekwentieverloop van de doppler-tonen duidelijk maakt, geven we hier opnieuw een 'driestemmige partituur' gemaakt vanuit de X,Y,Z kurves.
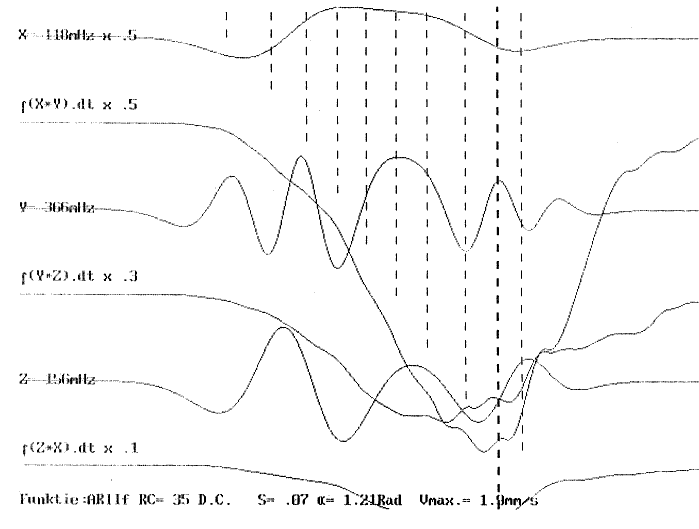



2.3.4.2: Metingen
2.3.4.2.1.: Oscilloskoop-afdrukken
Om technische redenen hebben we afgezien van onze oorspronkelijke bedoeling, op deze plaats uitgebreid verslag te geven van de 'elektronische werkelijkheid' zoals we die te zien krijgen op het scherm van onze oscilloskoop. Van onze H.F.-oscilloskoop konden we zonder grote investeringen op fototechnisch vlak geen schermafdrukken maken, terwijl anderzijds de komputer L.F.-skoop waarover we beschikken een veel te beperkte bandbreedte (de bemonsteringsfrekwentie is hooguit 20kHz) heeft om op een relevante wijze signalen op papier te brengen.We hopen dat de lezer zo welwillend zal zijn ons op ons woord te geloven wanneer we stellen dat de op het oscilloskoopscherm toonbare kurves in zeer hoge mate overeenkomen met de door onze simulator geproduceerde signalen. Overigens kunnen we dit ten allen tijde in het laboratorium demonstreren, en bovendien steunt de praktische uitwerking zoals we die beschrijven in het volgende hoofdstuk, geheel op deze analyzes.
2.3.4.2.4.: Overige meetgegevens:
Gemeten ruisspanning op de uitgang van de analoge komputer:- GMP konfiguratie : 10mVpp
- MMP konfiguratie : 6mVpp
De maximale uitgangsspanning van de analoge komputer -ingesteld als vermenigvuldiger zonder verdere nabewerking- (behalve uiteraard de filtering van niet relevante frekwentiegebieden) bij volledige uitsturing door de bewegingsdetektoren is:
- Upp = 26V of 9.12Vrms
| Signaal/Ruisverhouding: | MMP <= -72dB GMP <= -68dB |
| Deze metingen werden uitgevoerd gebruik makend van de oscilloskoop. De precisie is dan ook niet erg groot (ca. 20% fout). |
| Praktische ruisspanning: | MMP ≈ 110mVpp GMP ≈ 150mVpp |
- MMP <= -45dB
GMP <= -42dB
Technisch gesproken zijn we heel tevreden met dit rezultaat, omdat het een oplossend vermogen mogelijk maakt van bijna 8-bits, een waarde dus die in dezelfde grootte-orde ligt van 'ormale' muziekinstrumenten, en dus ook voldoet aan onze eisen geformuleerd bij het afsluiten van ons eerste hoofstuk. Ook blijkt in de praktijk dat het niet erg veel zin heeft enorme inspanningen te doen om de technische kwaliteit inzake dynamiek nog verder op te drijven, aangezien de ruisbijdrage voortkomend van praktische gebruiksomstandigheden een faktor 10 groter blijkt te zijn dan die van de gebruikte hardware.
2.4: Artistieke prezentatie als muziektheater
Van instrument naar kompositie ...Het is fascinerend te zien en te horen hoe zelfs de geringste trilling van een vingerkootje de hier gebruikte ultrasone geluidsgolven blijken te beinvloeden en hoe ze verschiltonen produceren die binnen het hoorbereik vallen. Op die manier is beweging niet langer alleen zichtbaar, maar is ze ook letterlijk hoorbaar geworden. Het instrument, eens de eerste prototypes werkten, leidde me, samen met mijn partner in het Logos-Duo, Moniek Darge, als het ware op een evidente wijze en vanuit zijn fascinerende eigenschappen tot het gelijknamige en uiteraard multi-mediale muziekstuk.
De ruimte tussen de zender en de ontvangers leek ons als het ware behekst.
Een viervlak of tetraeder werd de imaginaire ruimtelijke figuur, die deze zender en ontvangers met elkaar verbindt. De behekste ruimte werd verder ook gesymbolizeerd door twee rode koncentrische cirkels op de grond, die de in- en omgeschreven bollen van de tetraeder visualizeren.
Zodra de heksenkring wordt betreden, treedt de apparatuur in werking en wordt beweging geluid.
De uitvoerder 'danst' niet alleen maar kreeert tegelijkertijd zelf de muziek, want iedere verandering van snelheid en bewegings-richting zorgt voor toonhoogte- en geluidssterkte variaties. De drie signalen die opgevangen worden door de ontvangers, zijn immers elk volgens een andere vektor afhankelijk van de bewegingssnelheid en energie, zodat de uitvoerder eens binnen de heksenkring, een werkelijk onzichtbaar muziekinstrument lijkt te bespelen.
De tweede speler -en dat werd bijna als vanzelfsprekend mijn eigen rol- die roerloos buiten de cirkel achter de elektronische apparatuur zit, mengt deze drie signalen in onderling regelbare sterkteverhoudingen. Hij gebruikt dit mengsignaal als frekwentiemodulatie-signaal voor de ultrasoonzender, met als rezultaat dat er zgn. staande golven worden opgewekt. Deze golven zijn hoorbaar als geluiden die typisch en uniek zijn voor die bepaalde ruimte terwijl zij tevens op een spookachtige manier variëren naar gelang de omgevingsakoestiek.
Het komplexe oscillatiesysteem, dat binnen de eerste heksenkring wordt gebruikt, laat aldus toe een relevant akoestisch bewegingshologram te realizeren, wat bijvoorbeeld middels fotocellen of soortgelijke optische systemen niet kan.
Sinister en dreigend evenwel lokt de magische aantrekkingskracht van het centrum de performer. En uiteindelijk wordt ook de tweede cirkel betreden.
Een duivels metaalachtig geraas bestraft de indringer.
Het helse kabaal wordt veroorzaakt door de drie versterkte signalen die hiertoe elk afzonderlijk in een transducer worden gestuurd. Hun trillingen worden overbracht op bandveerstaal (Hasberg-meetlint) dat op zijn beurt de trillingen doorgeeft aan vier nieuwe trillingsopnemers.
De signalen van deze trillingsopnemers worden nu versterkt, bewerkt door een komputergestuurde "modulo-N deler/ vermenigvuldiger" en gemengd met het oorspronkelijk signaal.
Een deel van het signaal wordt rechtstreeks hoorbaar gemaakt, een ander deel wordt teruggestuurd naar de trillingstransducers. Door deze opstelling wordt een tweede meer-dimensioneel trillingssysteem gerealizeerd.
Een kringloop van duivelse klanken.
De performer zit letterlijk vastgeketend aan het geluid en stort machteloos neer in het centrum van de magische sferen,om als een phoenix uit vuur en as te herrijzen.
En, met dit 'plot' of noem je zoiets nu 'libretto' , is tevens ook de gehele partituur niet alleen beschreven maar ook geschreven. De verklanking is immers in het instrument ingebouwd.
2.5 Een eerste midi-implementatie
2.5.1- Holosound: Midi-versie
Gezien de vrij grote internationale belangstelling voor het hiervoor beschreven Holosound systeem, en ingaand op heel wat vragen van bevriende musici in die zin, bouwden we uitgaand van de bestaande front-end komponenten voor Holosound, in 1987, ook een eerste experimentele 'MIDI'-versie. Lange technische diskussies met vooral Joel Chadabe, komponist en tevens ook direkteur van het softwarebedrijfje 'ntelligent Musical Systems', hebben geleid tot het vaststellen van de wenselijke specifikaties voor het gebruik van Holosound als midi-controller.
Joel Chadabe was hoogleraar aan de Buffalo State University, maar gaf zijn positie op om zich in het meer lukratieve ontwikkelen van software voor musici te storten. - De output van het toestel diende data te zijn in het gestandaardizeerde midi-formaat, dus, status-byte + kanaalinformatie (8-bits) gevolgd door data (1 of 2 7-bit bytes). In deze implementatie worden dus niet de verschiltonen rechtstreeks hoorbaar gemaakt, maar komen zij als reeksen numerieke waarden op de midi-uitgang beschikbaar om andere klankopwekkings- of verwerkingsapparatuur aan te sturen. Deze holosound implementatie presenteerden we in een technisch paper en technische demonstratie op de 'International Computer Music Conference' in Keulen in september 1989. Voor de omzetting wordt uitgegaan van de hiervoor beschreven analoge komputer blokkendoos-schakeling. Uit de drie door de analoge komputer geleverde signalen worden telkens twee voor gebruik als kontroller relevante parameters (intensiteit en frekwentiedichtheid) in digitale vorm omgezet. Voor wat betreft de intensiteit gebeurt dat in het ontwerp door het signaal in hardware te integreren, waarna de omhullende overblijft, en het dan via eenvoudige ADC's met een rezolutie van 8 bits om te zetten. De frekwentiedichtheid -deze term past hier beter dan 'frekwentie' gezien het kleurruiskarakter van het signaal- wordt uit het signaal afgeleid door het eerst te differentieren en om te zetten in een reeks pulsen, die dan worden geteld. Men merke wel op dat het hier absoluut niet om een periodiek verlopend signaal gaat. Het teller-rezultaat - dat steeds waarden tussen 0 en 127 oplevert omwille van de midi-kompatibiliteit- is dan direkt als digitale informatie beschikbaar. Alle digitale signalen hebben een rezolutie van 7 bits. Voor de ADC's wordt het LSB dus niet gebruikt. Hiervoor werd geopteerd omdat dit een erg eenvoudige aanpassing aan het midi-kommunikatieprotokol mogelijk maakt . In totaal levert deze holosound-midi-convertor dus een reeks van 6 bytes van 7 bits en wel alsvolgt: byte 1 : pitch counter value 0 - 127 channel 1 byte 2 : intensity value 0 - 127 channel 1 byte 3 : pitch counter value 0 - 127 channel 2 byte 4 : intensity value 0 - 127 channel 2 byte 5 : pitch counter value 0 - 127 channel 3 byte 6 : intensity value 0 - 127 channel 3 Om eenvoudige interfacing naar bestaande apparatuur mogelijk te maken voorzagen we in het ontwerp 10 supplementaire bytes die door het interface kunnen worden uitgestuurd en waarvan de inhoud vrij bepaald kan worden door programmering in een Eprom. Volgende output-sekwens kon dan ook heel eenvoudig geimplementeerd worden: byte 1 : ROM-based &HC0 programm change channel 1 byte 2 : ROM-based &Hxx programm number byte 3 : ROM-based &H90 NOTE ON info channel 1 byte 4 : converter pitch-byte channel 1 byte 5 : converter intensity-byte channel 1 byte 6 : ROM-based &HC1 programm change channel 2 byte 7 : ROM-based &Hxx programm number byte 8 : ROM-based &H91 NOTE ON info channel 2 byte 9 : converter pitch-byte channel 2 byte 10: concerter intensity-byte channel 2 byte 11: ROM-based &HC2 programm change channel 3 byte 12: ROM-based &Hxx programm number byte 13: ROM-based &H92 NOTE ON info channel 3 byte 14: comverter pitch byte channel 3 byte 15: converter intensity byte channel 3 byte 16: ROM-based &HFF not used De volgorde waarin de bytes worden uitgestuurd kan eenvoudig via de hardware worden ingesteld. (middels jumpers op het PC-board). Alle dataverwerving in het interface systeem verloopt volledig synchroon met de 1 MHz klok, waaruit ook de midi-baud-rate wordt afgeleid. De tijd die het interface nodig heeft om een cyclus van 16 bytes uit te sturen is 64ms. Dit komt neer op een midi-informatie verversingstempo van maximaal 15.6 keer per sekonde. Blokschematisch gezien is het interface opgebouwd alsvolgt :De ingangssignalen zijn afkomstig van de drie audiokanalen die beschikbaar zijn uit de hiervoor beschreven apparatuur voor Holosound, de analoge komputerschakeling dus. Gezien de non-periodiciteit van de opgewekte signalen kon geen gewone frekwentiemeting worden toegepast, maar gebruikten we een teller die synchroon met de uitgangen van de ringteller ( 1/8ste van de klokfrekwentie dus) wordt gereset en met tellen herbegint. De ADC wordt hier gestuurd door een low pass-filter dat eigenlijk als enveloppe follower werkt (de afsnijfrekwentie is in de orde van de 0.2 Hz ). Ook deze ADC wordt door de ringteller gestart en gereset. De zes 7-bits parallelle uitgangen samen met 10 in EPROM-vastgelegde bytes worden dan om beurten naar een UART gestuurd die er een serieel midi-signaal van maakt.
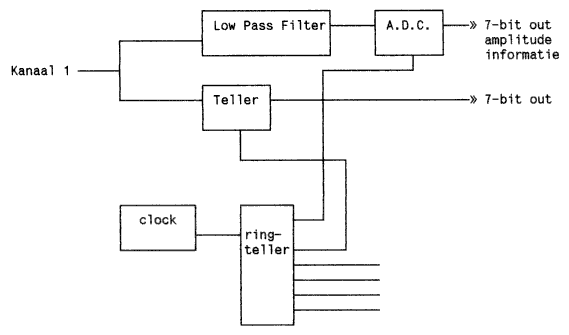
2.5.2 - Evaluatie en kritiek
Hoewel we enorm veel tijd en energie staken in de ontwikkeling van dit ontwerp, hebben we er nooit ook maar enige artistieke toepassing voor gevonden. Het was en bleef een speeltuig, dat door het bijna banale en al te voorspelbare van zijn klankrezultaat door mij als speelgoed werd ervaren.
Een van de vele problemen met deze, volledig in hardware gerealizeerde omzetting van holosound informatie naar midi-bytes, bleek de uiterst geringe flexibiliteit van het systeem te zijn. Althans, voor niet hardware-technisch kompetente gebruikers. In het jargon noemt men dit user-fiendly... Estetische ingrepen op het rezultaat zijn hier alleen mogelijk wanneer we de midi-output van de schakeling, via een komputer verder algoritmisch en kompositorisch gaan verwerken. Maar dit vertraagt de werking van het systeem aanzienlijk. Immers de data worden als MIDI-bytes ingelezen, verwerkt en opnieuw als MIDI-gegevens uitgestuurd. De hele reden om het interface rechtstreeks MIDI-informatie te laten genereren vervalt dan immers.
Gepoogd werd de midi-bytes te gebruiken als een 'ontroller' zoals een pitch-bend wheel, een portamentopedaal... een toepassing waarvoor minimale wijzigingen in de inhoud van de EPROM volstonden. Dit leverde echter nogal wat problemen op met de integratie met andere apparatuur. Immers midi-datastromen dienen zich te houden aan een strikt vastgelegd serieel protokol, waardoor bvb de data-sekwens kanaal/noot-aan , noot-byte, aanslag-byte, niet mag onderbroken worden door bytes afkomstig van een of andere 'ontroller'. Het bleek voor dergelijke toepassingen noodzakelijk een 'intelligente' midi-combiner-schakeling toe te voegen. De estetische eenvoud van het ontwerp kwam daardoor in het gedrang. Immers zo' 'ombiner' is op zich een kleine komputerschakeling, die alweer een extra brok hardware én software omvat. Er moet dus geprogrammeerd worden... De overgang naar een volwaardige komputerversie drong zich op.
Om aan de vele bezwaren verbonden aan deze eerste hardware-matige digitale implementatie te verhelpen ontwierpen we dan in 1991/1992 een volledig nieuw 'dedicated computer-system' dat alle door voorgaande schakeling uitgevoerde omzettingen in software realizeert en bovendien tegelijkertijd voor de kompositorische verwerking instaat. Maar, dit vormt het onderwerp van ons derde hoofdstuk.
Foto van de gerealizeerde gedrukte schakeling voor de Holosound-midi konverter:

Foto van de analoge komputer zoals gebruikt in de kompositie 'Holosound' (versie 1987).
2.6.: Besluit:
We menen in dit hoofstuk de doelen 1 tot 6 gesteld bij het begin ervan te hebben gehaald.
Bovendien hopen we erin te zijn geslaagd de lezer ervan te overtuigen dat de door ons ontwikkelde muziektechnologie in staat is van een motorische beweging de globale essentiele parameters bewegingsmassa en bewegingssnelheid vektorieel te korreleren aan een audiosignaal. Vooral het idee om deze parametrische analyze uit te voeren met behulp van een analoge komputer -meer bepaald een analoge vermenigvuldiger- kan een bijdrage zijn tot de bruikbaarheid van de beschreven technologie voor het wetenschappelijk onderzoek naar motorische expressie.
De beschreven technologie voldoet principieel aan de eisen inzake rezolutie, geformuleerd in ons eerste hoofdstuk.
Beschouwd als muziekinstrument is 'Holosound' een mislukking omdat de erdoor voortgebrachte geluiden geen de minste programmeerbaarheid hebben en bovendien dermate specifiek zijn (ruisbanden) dat ze los van de artistieke toepassing die wij ermee uitwerkten, op geen enkele meer algemene organologische bruikbaarheid kunnen bogen.
Onze praktische ervaring met Holosound, die overigens volledig bevestigd wordt door de analytische kurves voortgebracht door onze simulator, toont aan dat een eenvoudige parametrisch korrelerende omzetting van niet-positionele motorische parameters in geluidsparameters, niet leidt tot op zichzelf staande muzikale expressie. Een klankopname van Holosound is dan ook volstrekt ongenietbaar. Dit wordt in ons volgend hoofdstuk verder -in positieve zin dan- uitgewerkt.