Godfried-Willem Raes
'Magische Vierkanten'
'Magic Squares'
a suite of mappings for large robot orchestra
2024-2025
duur: ca. 36'
Susanne Langer beschreef muziek als een onvoltrokken taal, een syntactisch gevormde taal waaraan de semantische verwijzing naar de wereld geheel ontbreekt. Inderdaad, muziek verwijst uitsluitend naar interne toestanden van het menselijk bewustzijn. Die 'internal states of mind' kunnen enerzijds bestaan uit onze ervaringen en emotionele toestanden en anderzijds uit zuiver abstrakte koncepten. Tot die laatste behoren alle objekten die door de wiskunde worden beschreven. Niet alleen meetkundige figuren maar evenzeer algebraische vergelijkingen en algoritmen. Muziek die zich tot doel stelt die abstrakte koncepten muzikaal tot uiting te brengen door hen te verklanken, zouden we dan ook met recht en reden 'objektieve' muziek kunnen noemen. Muziek dus, waaraan individuele pathos geheel vreemd en die ontdaan is van alle emotie. Net zoals heel wat van mijn komposities, behoren ook deze reeks magische vierkanten tot de meest abstracte muziek die we ons zowat kunnen voorstellen.
Magische vierkanten zijn een 'Spielerei' uit de rekenkunde waarbij vierkante matrixen gevormd worden zo dat de som van de verschillende getallen in de rijen zowel als de som van de getallen in de kolommen telkens eenzelfde getal oplevert. Bovendien geldt dit ook voor de som van de getallen op de diagonalen van de matrix. Het aantal rijen en kolommen noemt men de orde van het magisch vierkant, sigma is dan de kenmerkende som van rijen en kolommen.
MSQ1
Het zal onmiddellijk duidelijk zijn dat voor orde 1 het magisch vierkant de uiterst triviale vorm 1 aanneemt. Onze verklanking ervan bestaat dan ook uit een enkel unisono op C#, overeenkomstig 1 MOD 12 = 1. De C# doorloopt daarbij wel alle mogelijke oktaafliggingen. Aangezien de laagste ligging buiten het gebied van het hoorbare valt, trommelen we die aan het tempo overeenkomend met C#0. We doopten het stukje MSQ1.
Download/beluister audio-bestand MP3
MSQ2
Voor orde 2 krijgen we te maken met een principiele onmogelijkheid omdat niet aan de voorwaarde kan worden voldaan dat de getallen in de matrix verschillend moeten zijn. Wanneer we deze voorwaarde echter zouden laten vallen, dat wordt het vierkant triviaal, want dan geldt het voor alle getallen. Vanwege de onmogelijkheid van dit vierkant, verklankten we dit middels stilte en maakten we hier uitsluitend gebruik van de licht- en bewegingsmogelijkheden van de robots. Het werd MSQ2.
MSQ3, 'saturnus'
Vanaf orde 3, krijgen we te maken met allerlei magische vierkanten die in de menselijke beschavingsgeschiedenis tot duizenden jaren terug gaan. Het eenvoudigste magisch vierkant met orde 3 heeft sigma 15 en vinden we terug bij Lo Shu in China en -met sigma 72- bij Kubera-Kolam in India.
Orde 3, sigma 15:
8 3 4 1 5 9 6 7 2 tellen we in alle cellen 19 bij, dan krijgen we het orde 3 sigma 72 vierkant:
23 28 21 22 24 26 27 20 25 Een magisch vierkant opgebouwd met uitsluitend priemgetallen blijkt ook mogelijk. Hier een orde 3 sigma 177 vierkant met uitsluitend priemen:
Het merkwaardige met dit vierkant is, dat wanneer we de getallen als midi-noten interpreren, we slechts 1 enkel interval terugkrijgen, namelijk de tritonus B-F.
Deze drie vierkanten kombineerden we tot een stukje van 2'51" onder de titel MSQ3, hoewel het ook MSQ3.15-72-177 had kunnen zijn.
MSQ4.33
Magische vierkanten orde 4, laten meteen ook heel wat meer mogelijkheden en variaties zien. Ook deze kennen een heel lange geschiedenis.
Een uitwerking van het magisch vierkant voor het getal 33, dat in de Schotse maconieke ritus -uiteraard afgeleid van het nieuw testament in de bijbel- een belangrijke rol speelt. 33 is namelijk de leeftijd waarop de mythishe figuur Jezus zou zijn gestorven. Een uitwerking voor n = 4 van de formule c = (n(n^2 +1))/2)-1 levert 33 op voor c. Dit magisch vierkant ziet eruit alsvolgt:
Dit vierkant is o.m. terug te vinden in de gevel van de Sagrada Familia basiliek in Barcelona.
De som van de getallen in elke kolom, evenals in elke rij, is telkens 33. Ook de som van de diagonale getallen is 33. De mapping maakt gebruik van zowel de horizontale lezingen als van de vertikale die tot harmonische samenklanken aanleiding geven.
De konstruktie van dit vierkant rammelt aan vele kanten en het is duidelijk dat de door religieuze symboliek bedwelmde numerologen het magisch vierkant met sigma 34 hebben verkracht om tot 33 te komen waarvoor ze getallen dienden te herhalen: zo komen de getallen 14 en 10 tweemaal voor. Deze verklanking doopten we MSQ4.33
Download/beluister audio-bestand MP3
MSQ4.34, 'jupiter'
Het sigma 34 vierkant - dat we o.m. bij Albrecht Dürer weervinden in zijn ets Melencolia I uit 1514- ziet er zo uit:
een variant uit de 10e eeuw in India uit de Chantisa Yantra ziet er zo uit:
De verklanking werd MSQ4.34, waarin beide verschijningsvormen van het magisch vierkant in klank worden getoond. De indische variant is een vele opzichten perfekter dan die van Durer, omdat alle sub-vierkanten waaruit het is opgebouwd, ook eenzelfde sigma som opleveren.
Download/beluister audio-bestand MP3
MSQ5.65, 'mars'
De muzikale uitwerking van dit vierkant werd een palindroom. Een rustige aftastende wandeling doorheen het vierkant, met een hieratisch rustpunt hier en daar. Het centrale getal 13 speelt daarbij een speciale rol.
Download/beluister audio-bestand MP3
MSQ6.111, 'sol'
Voor de verklanking van dit vierkant, kozen we voor een luchtige 6/8 maat. Bijna alle rijen en kolommen leveren hier sterke dissonanten op, met uitzondering van kolommen 2 en 5. Samen met de tot dissonante vierklanken te herleiden kolommen 1= 6 en 4 = 3 gebruikten we die voor de bereiding van de slotkadens.
Duur: 1'
Download/beluister audio-bestand MP3
MSQ7.175, 'venus'
Dit magisch vierkant omvat 49 verschillende getallen waarbij de som van alle rijen en kolommen telkens op 175 uitkomt. Voor de verklanking ervan gebruikten we de kwarttoonsinstrumenten van het robotorkest: <Qt>, <Puff>, <Xy>< en <Tubi>. Alle even getallen mapten we op de 'gewone' getemperde kromatische toonladder terwijl de oneven getallen van de kwarttonen gebruik maken. Merk op dat de diagonaal links-boven naar rechts-onder een dalende kwarttoonsladder vormt.
22 47 16 41 10 35 4 5 23 48 17 42 11 29 30 6 24 49 18 36 12 13 31 7 25 43 19 37 38 14 32 1 26 44 20 21 39 8 33 2 27 45 46 15 40 9 34 3 28 Duur: 2'
Download/beluister audio-bestand MP3
MSQ8.260, 'mercurius'
Aangezien de 64 getallen waarmee we hier te maken krijgen, in het bereik 1 tot 64 liggen, besloten we voor de mapping alle getallen als midi-noten te interpreteren, maar dan wel twee oktaven naar omhoog getransponeerd. Een ostinato gedistileerd uit de diagonalen van het vierkant vertrouwden we toe aan de piano terwijl het maatcijfer met 8/4 voor de hand lag. Het tempo, MM130, maakt er een eerder vrolijke verklanking van.
Duur: 2'05"
Download/beluister audio-bestand MP3
MSQ9.369, 'luna'
Het magisch vierkant met orde 9 is gekenmerkt door de sigma som 369 en er zijn 81 verschillende getallen.
Voor de verklanking gebruikten we alle rijen -van links naar rechts en omgekeerd- evenals de diagonalen. De 41 als centraal getal bracht ons tot een tonale aantrekkingspool op F (Fa). In hoofdzaak maakt de orkestrale uitwerking gebruik van een orgel -in een tot 1 oktaaf beperkte tessituur- en de piano, omwille van de erg uitgebreide tessituur. Overige instrumenten worden gebruikt om de extreme intervallen te benadrukken. Een versie voor klein orgel (bvb. <Bomi>) en piano is ook perfekt mogelijk.
Duur: 3'00"
Download/beluister audio-bestand MP3
MSQ10.505
Het magisch vierkant met orde 10 is gekenmerkt door de sigma som 505 en er zijn 100 verschillende getallen. Omdat noten kleiner dan 15 door onze robots niet kunnen gespeeld worden, mapten we de getallen kleiner dan 15 op chromatisch berekende getemperde tempointervallen toegewezen aan <Casta2>, <Casta>, <Troms> en <Snar>. De verklanking begin bij de rechterkant van de bovenste rij en, na het bereikken van de laatste rij, klimt ze op via de diagonaal 87 - 100 om dan af te sluiten met de diagonaal 15 - 1.
100 89 79 65 53 46 33 27 12 1
82 22 68 47 10 91 58 32 76 19
77 34 43 7 11 90 92 56 69 26
39 41 2 14 78 25 88 94 60 64
44 9 13 80 66 36 21 86 95 55
6 17 30 35 42 59 67 71 85 93
57 97 81 23 38 63 75 20 3 48
61 52 98 84 28 73 16 8 45 40
24 70 54 99 83 18 5 49 31 72
15 74 37 51 96 4 50 62 29 87
Duur: 5'05"
Een opname is voorlopig nog niet beschikbaar.
Magische vierkanten met ordes 11 en 12 hopen we in de nabije toekomst nog uit te werken. De vierkanten zelf, geven we hier alvast:
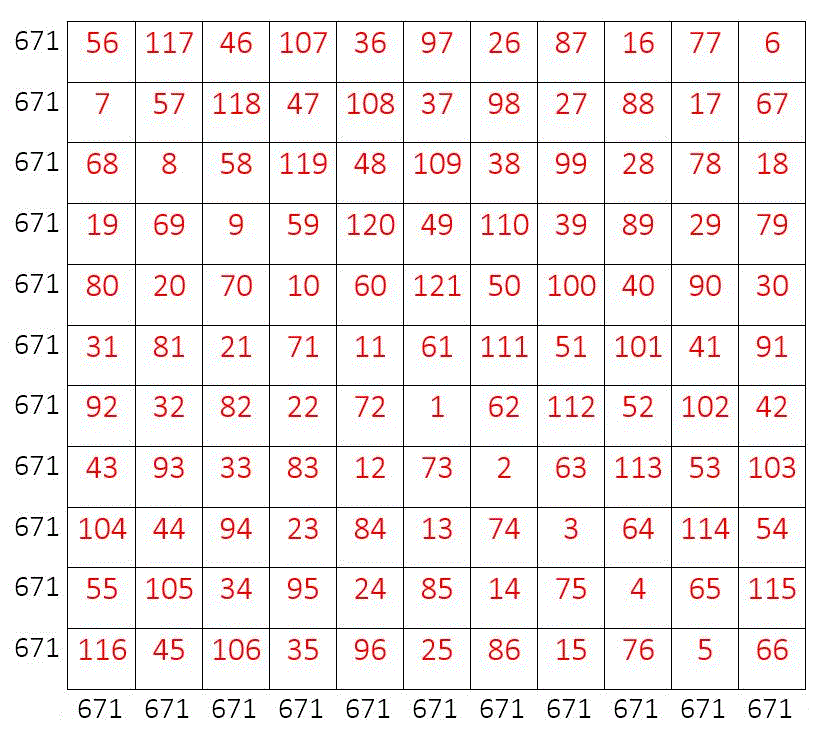
MSQ11.671
.MSQ12.870
5 8 33 36 121 124 77 80 105 108 85 88 [870]
6 7 34 35 122 123 78 79 106 107 86 87 [870]
28 25 128 125 12 9 100 97 92 89 84 81 [870]
27 26 127 126 11 10 99 98 91 90 83 82 [870]
21 24 1 4 137 140 93 96 73 76 101 104 [870]
22 23 2 3 138 139 94 95 74 75 102 103 [870]
116 113 144 141 16 13 44 41 72 69 52 49 [870]
115 114 143 142 15 14 43 42 71 70 51 50 [870]
133 136 17 20 117 120 61 64 53 56 45 48 [870]
134 135 18 19 118 119 62 63 54 55 46 47 [870.]
132 129 112 109 32 29 60 57 40 37 68 65 [870]
131 130 111 110 31 30 59 58 39 38 67 66 [870]
Gottfried-Wilhelm Leibniz: “Musik ist die versteckte arithmetische Tätigkeit der Seele, die sich nicht dessen bewußt ist, daß sie rechnet.”
De verschillende delen van deze suite kunnen en mogen ook afzonderlijk uitgevoerd worden. Ook de volgorde mag naar eigen inzicht en keus bepaald worden.
Gedeeltelijke Premiere (vierkanten 1 tot 9) : 19 december 2024, 20u00 : Logos Tetraeder Gent.
Volledige versie: 22, 23, 24 juli 2025, 20u00: Logos Tetraeder Gent, met een choreografie door Emilie De Vlam.
The scores may undergo some minor changes and updates in the near future.
Bibliografie:
Wikipedia, zoekterm 'Magic Square', laatst bezocht op 11.11.2024.
Cliffird A.Pickover, 'Het Wiskunde Boek', ed. Librero, zonder datum.