Kursus Experimentele Muziek: Boekdeel 2: Live electronics

<Naar inhoudstafel>

Een instrument, weze dat nu een louter technisch dan wel een muziekinstrument is steeds een verlengstuk van 's mensen fysische mogelijkheden. Het wezen van een muziekinstrument is gelegen in zijn overigens konfliktuele eigenschappen om enerzijds de expressieve mogelijkheden van zijn bespeler te verruimen, anderzijds echter, deze mogelijkheden op het vlak van de beheersing en de omgang in de weg te staan. De technische moeilijkheid om uit een bepaald instrument een bepaalde klank tevoorschijn te toveren draagt wezenlijk bij tot de expressieve betekenis van de geproduceerde klanken en van het musiceren zelf.

Vanuit deze min of meer filosofische ambivalentie vertrekt zowat al mijn kreatief werk op het vlak van konceptie en bouw van alternatieve muziekinstrumenten. Een derde facet dat - maar dit is dan geen algemeen geldige bewering met betrekking tot het muziekinstrument - van groot belang is in o.m. mijn werk , is de theatrale , of soms ook skulpturale, aanwezigheid ervan als fysisch objekt in beweging.

In de laatste jaren kwamen aansluitend bij vroeger werk op dit gebied vooral volgende nieuwe projekten op het vlak van de instrumentenbouw aan de orde :

• 1.- Holosound : het onzichtbaar instrument (1981-1988)
• 2.- HEX: de robot,de onbeheerste automaat (1986-1990), (cfr.2220)
• 3.- Talking Flames : (1989) (cfr.2130)
• 4.- A Book of Moves (1992) (cfr.2142)
• 5.- Songbook (1995)
• 6.- Holosound - Audio-Art installatie versie (1997)
• 7.- Slow Sham Rising (2000)

Wat ook al in min of meer sterke mate gold voor enkele van mijn vroegere instrumentenbouwprojekten (Pneumafoon, Klankboot, Toetkuip, Fingerbox) werd in deze projekten bijna extreem doorgedreven: nml. de specificiteit en intrinsieke verbondenheid van het instrumentarium met de muzikale kompositie waarvoor het werd ontworpen.

Organologen weten uiteraard beter dan wie ook, dat elk instrument getekend is door en in funktie staat van een bepaalde muziekhistorische periode en van de daarbinnen heersende muzikale stijlopvattingen en uitvoeringspraktijk. Ze zullen niet langer de vergissing maken , de geschiedenis van de (westerse) muziekinstrumenten te zien als beheerst door een trage evolutie naar een alsmaar groeiende universaliteit van deze instrumenten. Ze zullen ook niet spreken van als alsmaar toenemende 'perfektie' en verbetering van het instrumentarium (de piano als verbeterd klavecimbel bvb. )., omdat ze wel weten dat het instrumentarium en de muziek samen met hun makers in doorlopende beweging zijn.

Het adekwaat-zijn , of het doel-matig zijn, van een muziekinstrument is steeds een adekwaat zijn voor iets, en dat iets is nooit zomaar 'de muziek' in het algemeen. Wanneer dat iets overeenkomt met een bepaalde muzikale stijl, dan gebruiken we die stijl als epitheton bij de naam van dat instrument (vb. barok-fluit, jazz-gitaar... ). Wanneer echter het instrument alleen werd gebouwd voor de realisatie van een specifiek muzikaal idee, dan gaat het muziekinstrument samenvallen met de notie kompositie zelf , zeker wanneer dezelfde persoon voor de realisatie van beide instaat.

In de indonesische gamelan is dit overigens ook het geval : het woord gamelan slaat immers zowel op de voortgebrachte muziek als op het gebruikte instrumentarium.

Alle drie vermelde projekten, Holosound, Hex, Talking Flames, maken vergaand gebruik van hedendaagse elektronika, iets waarop ik me reeds van kindsbeen af heb toegelegd. Het zou evenwel verkeerd zijn te denken dat ze daarom ook maar iets met elektronische muziek te maken zouden hebben. Bij beide projekten wordt de elektronika immers uitsluitend gebruikt ter revelatie en als manipulator van zuiver akoestische trillingsverschijnselen in en van zuiver driedimensionele objekten.

Om dit duidelijk te maken, zal ik hier wat verder ingaan op de technische werking van het eerstgenoemde projekt.

Holosound is een instrument/kompositie dat iedere beweging van zijn bespeler vertaalt in klank. Het principe berust op wat ik ultrasone bewegingshologrammen heb genoemd.

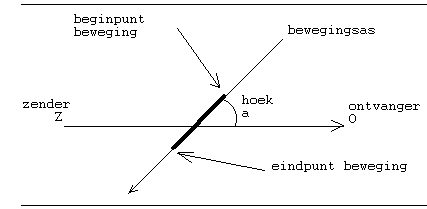
Een zender opgesteld op een bepaald punt in de ruimte stuurt ultrasone, dus onhoorbare geluidsgolven uit. Zolang binnen de door het geluid bestreken ruimte niets beweegt, gebeurt er niets en is er helemaal niets te horen. Vanzodra echter iets beweegt binnen de ruimte, dan wordt de ultrasone akoestische golf - afhankelijk van de richting van de beweging en haar snelheid, in frekwentie omhoog of omlaag gemoduleerd. De bespeler bevindt zich binnen deze ruimte en het is de oppervlakte van zijn lichaam in beweging die door het feit dat het klank reflekteert , oorzaak is van deze frekwentieverschuivingen. Dit principe berust geheel op wat men in de fysica het Doppler effekt heeft gedoopt.

Beschouwen we even de hand van de speler en laten we veronderstellen dat deze zijn hand aan een snelheid van 5 meter per sekonde rechtlijnig beweegt. Onderstel voorts dat de ultrasone zender een geluidsfrekwentie heeft van 100kHz. De frekwentieverschuiving gemeten in de richting van de beweging kunnen we dan berekenen alsvolgt :

• 1. stel de geluidssnelheid v=343m/s
• 2. relatieve geluidssnelheid in de richting van de beweging : 343m/s + 5m/s = 348m/s
• 3. procentuele verschuiving : 101,457% ( + 1,457%)
• 4. waargenomen frekwentie: 100kHz * 101,457% = 101.457Hz
• 5. Verschiltoon : 101.457Hz - 100.000Hz = 1.457 Hz

Merk op dat deze verschiltoon binnen het gewone audio-bereik valt! Maar, ook gezien vanuit de tegenovergestelde richting wekt de beweging een verschiltoon op ,nml :

• 2. relatieve geluidssnelheid tegen de richting van de beweging in : 343m/s-5m/s=338m/s
• 3. procentuele verschuiving : 98,54% (-1,46%)
• 4. waargenomen frekwentie: 100kHz * 98.54%=98.542Hz
• 5. Verschiltoon : 100.000 - 98.542 = 1.458Hz

Dit kan uiteraard ook in een stap berekend worden met volgende rekenkundige formule:

(1) f_diff=|(f_z*((v_g +v_b)/v_g))-f_z|

waarin dan:

• f_diff = de opgewekte verschiltoon
• f_z = de ultrasone zenderfrekwentie
• v_g = de geluidssnelheid
• v_b = de bewegingssnelheid

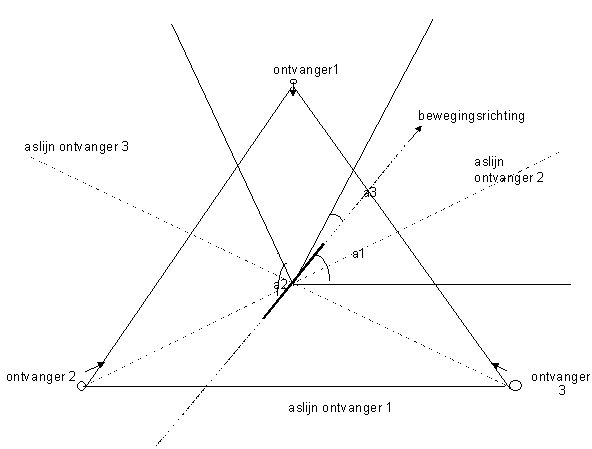
Hieruit blijkt dat de verschiltonen dezelfde frekwentie hebben wanneer de waarnemingspunten in het verlengde liggen van de richting van de beweging en dus onderling een hoek vormen van 180 graden. Om nu de richting van de beweging in klank om te zetten, volstaat het de waarnemingspunten onder een andere hoek op te stellen. Na wat rekenwerk blijkt dat een opstelling van waarnemingspunten onderling en ten opzichte van de zender onder een onderlinge hoek van 60 graden, een optimale ruimtelijke differentiatie mogelijk maakt.

De (vereenvoudigde) wiskundige vergelijkingen voor de som en verschiltonen worden dan afgeleid alsvolgt :

virtuele snelheid van de beweging gezien vanuit O:

fo1=fmax * |cos a|

Beschouwen we nu onze opstelling binnen een gelijkzijdige driehoek waardoorheen de beweging plaatsgrijpt en noemen we de bewegingshoeken vanuit elke ontvanger o1, o2, o3, dan a1, a2, a3 dan volgen de diverse frekwenties en hun samenhang uit :

en, wanneer we voor a1, a2 , a3 telkens alleen de scherpe hoeken beschouwen: 

en dus geldt ook :

fmax is hierin dan de frekwentie van de verschiltoon zoals we die zouden kunnen opvangen indien de beweging loodrecht zou staan op de as van een ontvanger. Zij valt eenvoudig te berekenen uit de 'absolute' bewegingssnelheid en de vaste zenderfrekwentie.

Wiskundig kunnen hieruit dan volgende relaties (2) , (3) en (4) tussen de frekwenties onderling worden afgeleid:

Uit a₁+a_{3 = Pi/3}

 _{(cos(a1)*cos(a3))-(1/2) = sin(a1)*sin(a3)}

 _{(cos(a1)*cos(a3))-(1/2) = ((1-cos}²(a1_{))^(1/2))*((1-cos}²(a3_))^(1/2)

 _(cos²(a1_)*cos²(a3_{))+(1/4)-cos(a}1_)*cos(a3_{)= 1-cos}²(a1_)-cos²(a3_)+(cos²(a1_)*cos²(a3_{))  cos}²(a1_)+cos²(a3_)-(cos(a1_)*cos(a3_{) = 3/4}

₍₂₎ f1²+f3²- f1_*f3= (3/4) * fmax²

Voorts volgt uit a1 _{+ a}2 = (2/3)*Pi dat :

waaruit volgt:

(3) f₁²+f₂²+(f₁*f₂)=(3/4)*f_max²

Door nu (2) en (3) gelijk te stellen komen we tot een bijzonder en welhaast estetisch eenvoudig verband tussen de onderlinge toonhoogtes :

of:

of nog:

waaruit tenslotte volgt :

Technisch probleem dat zich onmiddellijk stelt wanneer we op grond van bovenstaande wiskundige overwegingen een instrument zouden willen bouwen, is dat de berekende verschiltonen niet akoestisch bestaan noch als dusdanig waargenomen worden door menselijke waarnemers. Hier diende dus de analoge elektronische rekentechniek ingeschakeld te worden. In eerste instantie poogde ik gebruik te maken van allerhande schakelingen zoals die werden ontwikkeld voor -overigens erg onbetrouwbare- alarmsystemen en dieptemeters uit de scheepvaarttechniek. Bijna al deze schakelingen berusten echter op een of andere vorm van amplitude-demodulatie (alarmen) of pulsvertragingstijdmeting (dieptemeters en echografen). De signalen worden in deze technische toepassingen immers alleen gebruikt om logische nivoos te genereren. Bovendien bleek de haalbare signaal/ruisverhouding voor muzikale doelen volkomen onaanvaardbaar. Na toch wel enkele jaren van nogal intensief laboratoriumwerk, heb ik uiteindelijk volgend schakelprincipe als optimaal weerhouden . De 'clou' van de schakeling bestaat enerzijds in het oneigenlijk gebruik van gebalanceerde modulatoren als frekwentie-demodulatie-schakelingen , voor een signaal dat eigenlijk geen echt frekwentiemodulatiesignaal is, en anderzijds in de manier waarop de demodulatoren onderling gekoppeld werden. Voor de niet-technische lezer kan ik wellicht volstaan door de werking van de gebalanceerde modulator te definieren als een elektronische schakeling die van twee op de ingangen aangeboden elektrische spanningen met een bepaalde frekwentie steeds alle som en verschiltonen tussen die frekwenties opwekt en op de uitgang aanbiedt. Ook de uit de vroegere elektronische muziek welbekende ringmodulator berust op deze schakeling.

De overdrachtfunktie van zo'n modulator ziet eruit alsvolgt:

voor twee sinusvormige ingangssignalen en U_x2=-U_x1 , U_y2=-U_y1 (dit is immers het geval wanneer de schakeling gebalanceerd wordt uitgestuurd ) wordt dit dan :

(5) U_out=(2*U_x1)*(2*U_y1)/10V

of nog:

(6) U_out=(2*(U_xmax*sin(2*Pi*f_x*t))*(2*U_ymax*sin(2*Pi*f_y*t)))/10V

In werkelijkheid krijgen we in deze toepassing echter niet twee signalen op de ingangen te zien, maar wel op elke ingang de som van twee signalen: de zenderfrekwentie plus het daaraan toegevoegd Doppler-verschoven signaal. De overdrachtfunktie wordt dan ook verkregen door in formule (5) de termen U_x en U_y te subsitueren door:

(7) U_x1= U_zmax*sin(2*Pi*f_z*t)+U_xmax*sin(2*Pi*f_x*t)

U_y1= U_zmax*sin(2*Pi*f_z*t)+U_ymax*sin(2*Pi*f_y*t)

waarin dan U_z en f_z resp. de ontvangen maximumspanning en de frekwentie van de draaggolf zijn, en U_x, f_x en U_y, f_y respektievelijk spanning en frekwentie van de Doppler-verschoven komponent in het signaal.

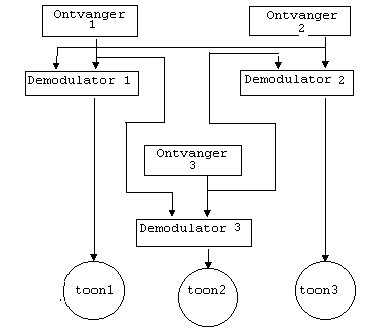
Het blokschema van de gehele schakeling werd:

De teoretische en sterk vereenvoudigde overdrachtfunkties voor deze schakeling zijn dan:

Uitgangssignalen van de ontvangers :

Ingangssignalen van de demodulators:

En dus , met gebalanceerde ingangssignalen :

Waarin : U_z , f_z :resp. spanning en frekwentie van de zender

Het gedrag van het systeem werd uitvoerig getest door een simulatie ervan in de vorm van een daartoe door mij geschreven komputerprogramma. Dit kon vrij makkelijk worden geschreven omdat de schakeling zelf eigenlijk een analoge komputer is. Hierbij kon rekening gehouden worden met de in funktie van de richting van de beweging veranderende verhoudingen van Ua,Ub en Uc evenals met de vaste wiskundige relaties tussen fa, fb en fc.

In het uitgangssignaal blijft een betrekkelijk sterke zendersignaalkomponent aanwezig, evenals heel wat nevenfrekwenties op veelvouden daarvan. Deze konden echter op eenvoudige wijze weggefilterd worden, gezien de grote afstand - in frekwentie - tussen het gewenste uitgangssignaal en deze bijprodukten.

De praktische opbouw van de schakeling wanneer men een muzikaal aanvaardbare signaal ruisverhouding wil halen in de orde van de 60dB stelt de uiterste eisen inzake precisie aan de gebruikte onderdelen en aan de afregeling. Voor de opbouw werd dan ook gebruik gemaakt van precisie instrumentatieversterkers en laser-trimmed analog multipliers van de firma Analog Devices (type AD632). Ook de bouw en ontwikkeling van de ontvangers was niet direkt een triviale aangelegenheid. Er bestaan weliswaar piezolektrische ultrasoon ontvangers in de handel (o.m. van Murata, Japan) , maar die zijn elektrisch zowel als mechanisch gestemd op een welbepaalde werkfrekwentie (meestal 40kHz) en hebben een betrekkelijk kleine bandbreedte en een enorme non-lineariteit. Twee bruikbare types kwamen na lang zoeken uit de bus : enerzijds mechanisch gedempte en elektronisch gelineariseerde piezoelelektrische ontvangers, anderzijds zelfgebouwde kondensatormikrofoons, waarvoor echter een nogal grote externe voedingsspanning nodig is waardoor ze moeilijk te miniaturiseren vallen. Op dit vlak kan verdergaand onderzoek wellicht nog veel aan de goede werking verbeteren.

Het instrument werkt in principe met eender welke ultrasone toonhoogte, waarbij het duidelijk zal zijn dat naarmate men deze toonhoogte hoger kiest, het frekwentiebereik van de ontstane verschiltonen ook groter zal zijn. Hier zijn echter zeer grote praktische beperkingen aan verbonden : immers naarmate men de toonhoogte laat stijgen is er , voor het bestrijken van een evengrote ruimte, een akoestisch afgestraald vermogen nodig dat niet evenredig stijgt met de toonhoogte, maar wel met (ongeveer) de vierde macht daarvan !

Bij de laagste in dit instrument bruikbare ultrasone frekwentie van circa 34kHz volstaat een elektrisch zendervermogen van 2 Watt ruimschoots.

Bij 200kHz is algauw zowat 35Watt nodig, en in de praktijk nog heel wat meer , wat dan te wijten is aan de geringe efficientie van ultrasone stralers in lucht bij deze frekwentie. Een bijkomend probleem is dat geluid naarmate de frekwentie toenoemt, direktioneler wordt afgestraald, wat nogmaals bijdraagt tot een noodzakelijke vermogensverhoging. Op een bepaald punt echter worden hierbij grenzen kwa ultrasone geluidsdruk overschreden waarbij helemaal niet meer voor zeker kan worden aangenomen dat ze voor de mens ongevaarlijk zijn.

Bovenstaande akoestisch-wiskundige en technische overwegingen zijn uiteraard sterk simplifierend . Zo dien ik er bvb. toch op te wijzen, dat het in werkelijkheid onmogelijk is om een 'zuivere' toon te produceren , maar dat steeds 'kleurruis' met min of meer duidelijke toonhoogte ontstaat. Dit laat zich makkelijk verklaren uit het feit dat waar we in onze aanvankelijke analyze uitgingen van een bepaalde bewegingssnelheid, dit in de praktijk niet kan bestaan. Immers , wanneer een mens een lichaamsdeel beweegt, dan beweegt elk punt ervan aan een verschillende snelheid : wanneer je met de armen zwaait blijven de schouders min of meer op hetzelfde punt. Derhalve zijn de voortgebrachte verschiltonen ook de som van alle gereflekteerde frekwenties, m.a.w. klusters.

Een tweede opmerking geldt het feit dat de sterkte van de opgewekte geluiden recht evenredig is met de grootte van het bewogen oppervlak. Dit effekt is echter muzikaal uitstekend te gebruiken omdat het perfekt aansluit bij de relatie expressie-beweging van de mens. Het instrument zet de snelheid van de beweging om in de toonhoogte van een kluster. Een lineaire beweging geeft aanleiding tot een min of meer konstante toon, terwijl een versnelling een stijgende glissando wordt, een vetraging een dalende . De intensiteit van de beweging ( de hoeveelheid lichaam die beweegt), wordt omgezet als de geluidssterkte van die kluster. Bovendien geschiedt alles vektorieel , d.w.z in funktie van de richting van de beweging.

Wanneer nu de luidsprekers waarop de resulterende klanken ten gehore worden gebracht in een driehoekige opstelling waarbinnen de luisteraar zich moet bevinden, dan hoort deze laatste als het ware akoestische bewegingshologrammen : de klanken -in funktie van de bewegingen die hen veroorzaken -bewegen zich overeenkomstig door de akoestische ruimte.

Een verdere mogelijkheid waartoe het instrument zich makkelijk leent, ontstaat wanneer we de zender uitvoeren als een ultrasone FM-zender, waaraan we een extern signaal als modulatiesignaal toevoeren. Gezien de aard van het instrument is als modulatiesignaal daarvoor de stem van de speler-beweger het meest voor de hand liggend. De toonhoogte van dit modulatiesignaal zullen dan in frekwentie veranderen in funktie van de beweging van de spreker/zinger.

Ook konfiguraties waarbij het uitgangssignaal wordt teruggekoppeld naar de modulatieingang van de zender, leveren verrassende muzikale resultaten op, die dan echter nagenoeg volledig afhankelijk zijn van de akoestische ruimte waarin het instrument wordt opgesteld. Op een dergelijk dynamisch systeem kunnen de klassieke lineaire wiskundige beschrijvingstechnieken niet langer worden toegepast , maar dienen we ons wiskundig apparaat in de richting van niet lineaire vergelijkingen te gaan zoeken . De Lorenz-vergelijkingen zijn daarvan naast de Mandelbrot Fractals uit de zgn. Chaos-theorie, wellicht de best gekende voorbeelden.

Die ruimte bepaalt overigens ook bij normale rechttoe-rechtaan werking in hoge mate het klankresultaat. De bedoelde en in het instrument geimplementeerde funkties komen theoretisch slechts korrekt uit de bus, wanneer we het instrument gebruiken in het akoestisch vrije veld (in een vlakke onbebouwde ruimte), of in een anechoische ruimte.

Het is fascinerend te zien en te horen hoe zelfs de geringste trilling van een vingerkootje de benutte geluidsgolven beinvloeden en verschiltonen produceren die binnen het hoorbereik vallen. Op die manier is beweging niet langer alleen zichtbaar, maar is ze ook letterlijk hoorbaar geworden. Het instrument , eens de eerste prototypes werkten, leidde me, samen met mijn partner in het Logos-Duo , Moniek Darge , als het ware op een evidente wijze en vanuit zijn fascinerende eigenschappen tot het gelijknamige en uiteraard multi-mediale muziekstuk.

De ruimte tussen de zender en de ontvangers leek ons als het ware behekst.

Een viervlak of tetraeder werd de imaginaire ruimtelijke figuur, die deze zender en ontvangers met elkaar verbindt. De behekste ruimte werd verder ook gesymboliseerd door twee rode concentrische cirkels op de grond , die de in- en omgeschreven bollen van de tetraeder visualiseren.

Zodra de heksenkring wordt betreden , treedt de apparatuur in werking en wordt beweging geluid.

De performer 'danst' niet alleen maar kreeert tegelijkertijd zelf de muziek, want iedere verandering van snelheid en bewegings-richting zorgt voor toonhoogte- en geluidssterkte variaties. De drie signalen die opgevangen worden door de ontvangers, zijn immers elk volgens een andere vektor afhankelijk van de bewegingssnelheid, zodat de performer eens binnen de heksenkring een onzichtbaar muziekinstrument bespeelt.

De tweede speler - en dat werd bijna als vanzelfsprekend mijn eigen rol - die roer-loos buiten de cirkel achter de elektronische apparatuur zit, mengt deze drie signalen in onderling regelbare sterkteverhoudingen. Hij gebruikt dit mengsignaal als frekwentiemodulatie-signaal voor de ultrasoonzender, met als resultaat dat er zgn. staande golven worden opgewekt. Deze golven zijn hoorbaar als geluiden die typisch en uniek zijn voor die bepaalde ruimte terwijl zij tevens op een spookachtige manier varieren naar gelang de omgevingsakoestiek.

Het komplexe oscillatiesysteem, dat binnen de eerste heksenkring wordt gebruikt, laat aldus toe een relevant akoestisch bewegingshologram te realiseren, wat bv. middels fotocellen niet kan.

Sinister en dreigend evenwel lokt de magische aantrekkingskracht van het centrum de performer. En uiteindelijk wordt ook de tweede cirkel betreden.

Een duivels metaalachtig geraas bestraft de indringer.

Het helse kabaal wordt veroorzaakt door de drie versterkte signalen die hiertoe elk afzonderlijk in een transducer worden gestuurd. Hun trillingen worden overbracht op bandveerstaal dat op zijn beurt de trillingen doorgeeft aan vier nieuwe trillingsopnemers.

De signalen van deze trillingsopnemers worden nu versterkt , bewerkt door een computergestuurde "modulo-N deler / vermenigvuldiger " en gemengd met het oorspronkelijk signaal.

Een deel van het signaal wordt rechtstreeks hoorbaar gemaakt , een ander deel wordt teruggestuurd naar de trillingstransducers. Door deze opstelling wordt een tweede meer-dimensioneel trillingssysteem gerealiseerd.

Een kringloop van duivelse klanken.

De performer zit letterlijk vastgeketend aan het geluid en stort machteloos neer in het centrum van de magische sferen,om als een phoenix uit vuur en as te herrijzen.

En, met dit 'plot' of noem je zoiets nu 'libretto' , is tevens ook de gehele partituur niet alleen beschreven maar ook geschreven. De verklanking is immers in het instrument ingebouwd.

Dit stuk is wellicht een van de meest uitgevoerde stukken Vlaamse eigentijdse muziek uit het laatste decennium, en werd zowat overal ter wereld opgevoerd. Het kende tot 04/03/90 alleen al niet minder dan 112 uitvoeringen! 

<Naar inhoudstafel>

<Naar verder onderzoek: midi en komputerversies>

<Naar 'A Book of Moves'>

Naar homepage dr.Godfried-Willem RAES